A few random numerical experiments

How fast and accurate is your FX TARF pricing engine? (Part 4) Download this demo to compare notes!

11/27/2025

Revisiting this series after some time, I ended up debugging and polishing a bit the UI I had built to facilitate my previous numerical experiments. So that it is now, hopefully, in good enough shape for anyone interested to download and play with.

This is obviously not intended to price real world deals. Its purpose is rather to provide a reference for what sort of performance (accuracy/CPU time) one can expect from a carefully implemented PDE-based pricing engine. In short, aiming for 1 bp accuracy should be achievable in milliseconds on a modern CPU core, not seconds.

You can use this app to visualize the solution discretization error, just like I did when I was refining the engine. First calculate a benchmark price by setting the grid resolution to something like [1000, 500] for [spot, time] and choose the “CN++” scheme (this would be practically grid-converged). Press Ctrl+R to save this as the reference solution. Then switch to a working resolution and scheme, like [100, 250] and "CN+", price and press Ctrl+X to visualize the discretization error along the spot axis.

Calculating benchmark prices is very fast (should be in seconds still), especially for the Black Scholes (BS) model. This is very useful for testing the basic convergence properties of the implementation. Given the complex structure of the product, it is the details of the FD discretization that can make a big difference in terms of convergence and thus performance, even for the simplest model. Achieve good BS behavior first and then switch to the target model. This demo can easily (in most cases) achieve 10 significant digits of numerical accuracy when you rev it up. Yes really, it is a well oiled engine!

The Local Volatility Model (LVM) brings things closer to industry standards, in case someone dismisses the BS performance as irrelevant. I haven't stress-tested this. Let’s just say that it worked well for the few FX surfaces I found (produced smooth LV surfaces and very tight fits to the vanilla market). Just assume that some properly tested, production-grade LV module can be used instead. The main purpose here is to establish that introducing (S, t)-dependent diffusion coefficients does not significantly affect the PDE discretization's efficiency. The FX volatility surface and zero rate curves are simply read in from a text file. Just replace the data in the file with your data, keeping the same format.

The LVM on its own will still be deemed inadequate in most cases for trading/risk-managing such a product. But an upgrade of the present setup to regime-switching local volatility (RSLV) would fix that, while inheriting the high-performance characteristics. Assuming for instance 3 regimes, we would expect the computational cost to triple, keeping accurate valuation times still in the milliseconds on average. To be confirmed in an upcoming update of the demo adding RSLV pricing once I find some time to test it.

I’ve included a quasi-Monte Carlo engine as well for peace of mind, to facilitate cross validation.

I hope you find this interesting, I certainly enjoyed working on every detail that makes it tick. For more usage details please read the README file that comes with the app before using it. Also do not hesitate to contact me with any queries and to report any bugs or problems you may find.

Yiannis Papadopoulos, Zurich, November 2025

January 2026 EDIT: As promised, the Regime-Switching Local Volatility model (with 3 regimes) has been added to v0.9.3. Note that this currently comes without a calibration module, the main purpose again being to verify that pricing efficiency is carried over from the previous models without significant penalty. And indeed, at least initial testing seems to confirm this. Randomized valuations using a few sample (major pair) IV surfaces show that the CN+ scheme with [100, 250] [spot, time] resolution would be sufficient for keeping errors below 1 bp. Single-core CPU timings, for example of 1Y TARF's with weekly fixings, are between 150-200 milliseconds. For higher vol levels (exotic FX, precious metals) the temporal resolution has to be increased to target the same error. Again, please check the README file for explanation on the inputs.

This now effectively has the core specs of a production-grade pricer. However it has obviously not been tested to production standards; this would require access to long series of market data and calibration for the RSLV. There will no doubt be some challenging inputs leading to larger errors, especially perhaps when it comes to precious metals. That said, the pricing engine is inherently "fast-converging” and a modest increase in resolution should be sufficient to bring errors down. Experience with actual market data would also allow customizations and fine-tuning. I may supplement this post with more specific testing results later on.

Efficient FX TARF pricing demo v0.9.3 (Windows)

P.S. If when running it for the first time you see ‘Windows protected your PC’, click ‘More info’ → ‘Run anyway’. This is expected — the app is signed with a local demo certificate.

0 Comments

How fast and accurate is your FX TARF pricing engine? Part 3: I asked ChatGPT to optimize the finite difference engine (and it worked)

8/13/2023

0 Comments

OK, so I lied to get your attention. You are presumably still interested in either TARF's, finite differences, or Deep Neural Networks and I have some original research here for you, so keep please reading!

ChatGPT of course is not quite there yet and will likely not be any time soon since this is a specialized application for which code is never public. But we can train our own "AI" to learn the FD engine's behavior and then use it to optimally set it up. More specifically, I am going to train it so that it can propose the optimal grid (or mesh if you prefer) construction for each pricing case (contract and market data).

It is in general more computationally efficient to use non-uniform grids that are denser near some point of interest, so that the solution is better resolved there (and less resolved in other areas where we don't care for). In option pricing that can be for example the strike, a barrier, or the spot. This makes the implementation slightly more involved but we can get more accuracy than with uniform grids for the same computational cost, or equivalently the same accuracy for lower cost. This is not a one-size-fits-all solution though. Different problems benefit from different degrees of non-uniformity, as well as choice of focus/cluster point(s) and one does not know a priori how to make these choices optimally. Not only that, some choices may lead to worse accuracy than what we would get using a uniform grid! And this is something that I have always found somewhat frustrating, using a more sophisticated tool with higher inherent accuracy without the ability to "calibrate" it.

But this is 2023 and AI can do almost everything, right? Of course some fear that it will destroy humanity. Others just see it as the new thing that will get them jobs or promotions. Me being naturally curious I had to look into it and at least have some first hand experience. Can it provide me with the (near-)optimal-grid picking tool I've been missing? Actually this is an idea I have meant to try out since I got interested in Neural Networks (NN's) a few years ago. It sounds good because it aims to enhance the traditional method without sacrificing mathematical transparency. After all we are only using the NN to decide on the grid, which we would otherwise do so more or less arbitrarily anyway. We just have to make sure that we let it choose from the range of options that we would and we are safe. As far as I am aware, this particular way of involving NN's in the solution of a PDE is novel, so I am trying out an oiginal idea here.

Now depending on the product to be priced, the grid construction may be simple or more complex. For example it may involve different segments and/or have to make sure certain values are represented by grid points. In my case the grid construction is key to the overall accuracy/efficiency of the engine. I am not going to get into the details here, but it does try to place points on the strike, the underlying level that would meet the remaining target and the spot (the latter only when it doesn''t result in too much stretching). Remember, the grid I am talking about here is the S-grid (i.e. the underlying, here some FX rate) that the 1-D solvers use (please see the first post in this series for a little bit more about the engine). The spacing between the accrued amount (A) planes to which each solver corresponds is also somehow derived from the S-grid. Despite this rather convoluted construction, at the heart of it the S-grid is based on the following well known stretching function:

$ S_i=S_{min}+K\left(1+sinh\left(b(\frac{i}{NS}-a)\right)/sinh(ab)\right)$

where K is the clustering point, NS the number of grid spacings and a, b are free parameters. b in particular controls the degree of non-uniformity and is the one we want to be able to choose optimally (as well as K) ; given b and K, a can then be determined so that the grid goes up to $ S_{max}$ (if interested see (1) for more details on employing such a grid).

The main idea:

We want to train a simple Artificial Neural Network (a Multilayer Perceptron) to "learn" the discretization error of the PDE numerical solution as a function of the PDE coefficients, initial and boundary conditions, plus some parameter(s) that drive the grid construction. Once we have a good (and very fast) NN approximation of the error, we can use it to solve for the grid parameters that would minimize it. So we can decide on the optimal grid construction before the actual numerical solution.

In this case, I have a PDE engine that solves for the fair value of an FX TARF contract. So the inputs to the functional of the output (the discretization error, from now on simply referred to as the "error") are the contract details, the market data, the parameter b of the grid stretching function and the clustering point K. Regarding the latter, in some cases it is preferable (meaning the solution error at S = spot, which is where we want the contract value, is lower) to focus the grid on the strike and in others on the spot. By the way, this whole grid selection process will take a fraction of a millisecond, so the added CPU cost will be negligible compared to the actual numerical solution which can take up to a second or more in the worst cases.

The goal here is to get more out of an existing solver. In practice one normally decides on some grid resolution (number of grid spacings in each dimension), so that the average error across all pricings is acceptably low. Remember this is a (pseudo) 2-D solver, we also have the accrued amount (A) planes grid. The number of planes NA will logically be proportional to NS, so the CPU time scales with ${NS^{2}}$. The discretization scheme will typically be second order accurate (in both space and time), so the error scales with $1/{NS^{2}}$, which means it is inversely proportional to the CPU time. So if enabling optimal grid selection can cut the average error of our current set-up in half, we should in theory be able to lower the resolution and get the same accuracy as our current set-up at half the CPU cost.

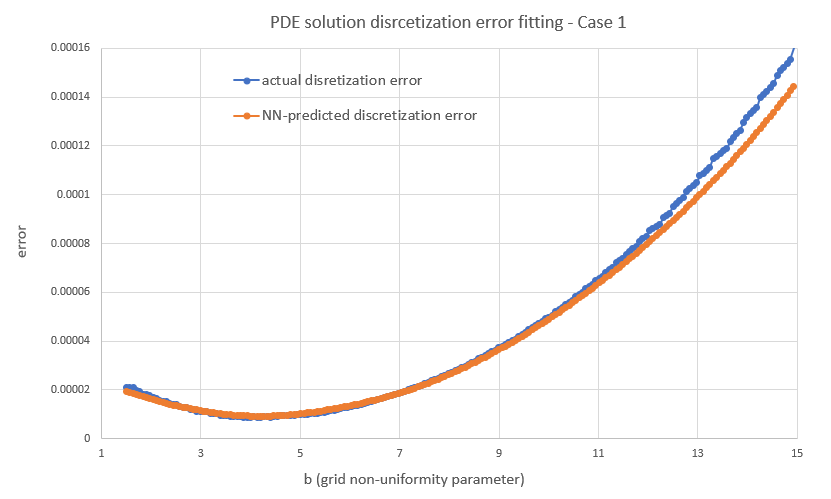
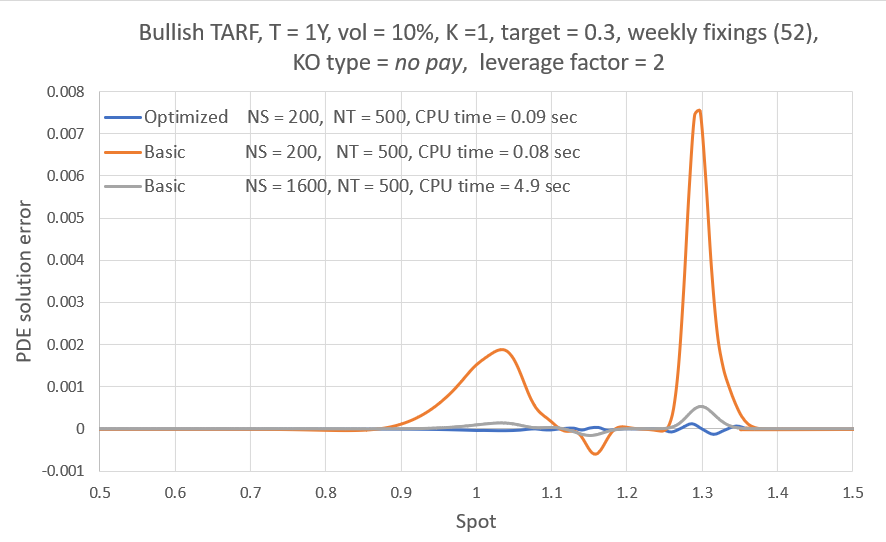
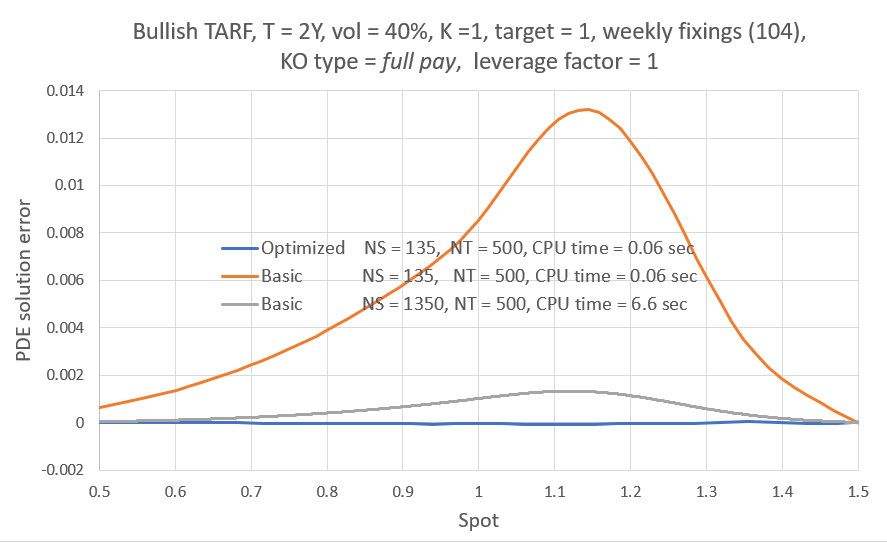
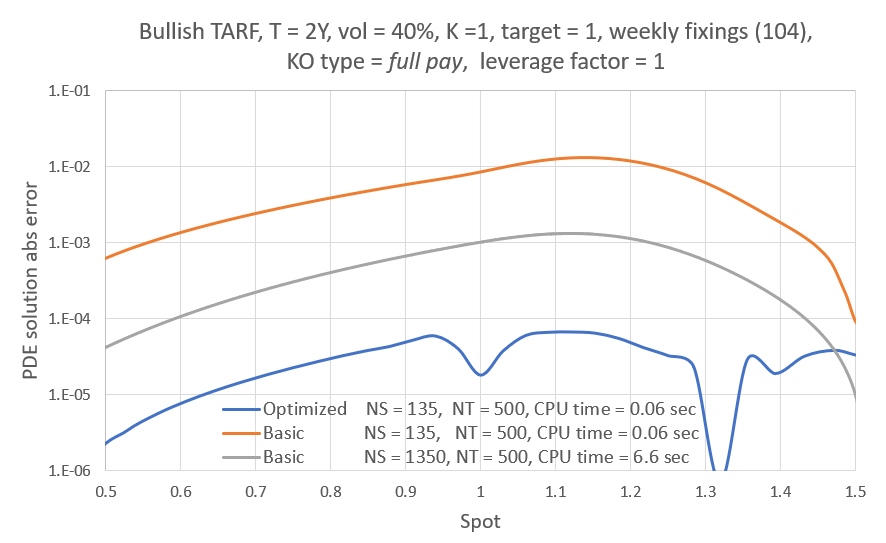
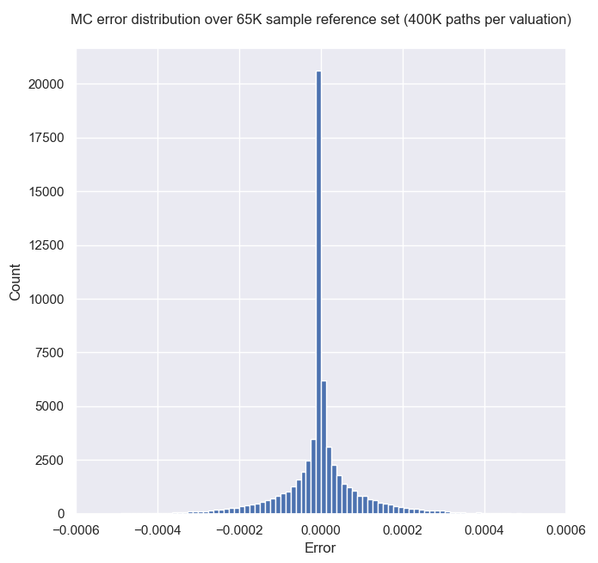
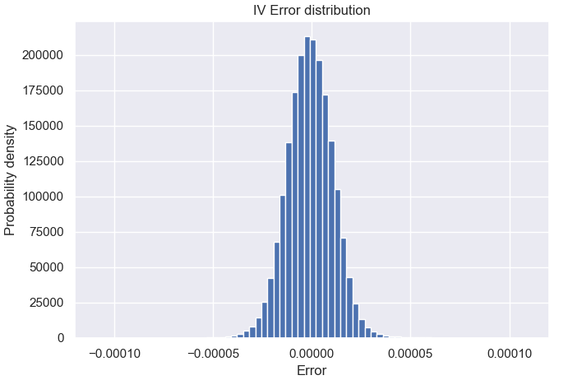
The error refers to some fixed working resolution (here NS=200) and it is calculated as follows: The PDE engine yields the TARF value on the grid points from which we find the value at the current spot $V_{Spot}^{NS=200}$either directly (if there is a grid point on the spot), or otherwise via $4^{th}$ order polynomial interpolation. We then repeat the valuation using a much finer (NS=900) grid (where the solution should be almost grid-converged) to find $V_{Spot}^{Ref}$. The error is then simply $\mid V_{Spot}^{Ref}-V_{Spot}^{NS=200} \mid $. For the reference valuation, K and b were chosen using a heuristic strategy I had in place for my previous two posts. Finally, I used a uniform time grid with NT=250 spacings/year for all valuations here, so the error has a temporal discretization component as well. Here though we are only focusing on fine-tuning the non-uniform "spatial" grid.

The Neural Network

I trained a small MLP (4 x 80 hidden layers) with a total of 524K samples, i.e. pairs of input vectors and output ( the error). The inputs and their considered ranges/possible values are shown below. Of course I also created a separate (smaller) test set to monitor the performance of the NN while training it. The inputs for both training and test sets were sampled uniformly from their respective ranges (either continuously or discretely where applicable), with the exception of the spot (lognormal).

Note that I have switched from using the local volatility model in the previous post, back to constant (BS) volatility here. The reason is just to facilitate my training, since otherwise I would have needed to create (valid) random volatility surfaces and I didn't want to go there for the purposes of this post. It is my view that this wouldn't have been significantly more difficult (if you have the machinery to generate random volatility surfaces at hand). As mentioned in the previous post, the pricing CPU time is the same and I fully expect the NN to be able to capture the error behavior in that case just as well as it does here for constant volatility. Something for the future perhaps.

DNN Input parameters
T (yrs)	0.001 - 2.5
target / strike	0.0001 - 1
leverage factor	0, 1, 2
KO type	0, 1, 2 (No pay, capped pay, full pay)
trade direction	0, 1 (bullish, bearish)
num. fixings	weekly or montly freq., remaining fixings follow from T
volatility	2% - 50%
spot / strike	lognormal (0, vol * sqrt(T))
r_d	-1% - 10%
r_f	-1% - 10%
b (grid non-uniformity)	1.5 - 15
K (grid cluster point)	0, 1 (strike, spot)

By the way, a value b = 1.5 results in a near-uniform grid, while b = 15 makes the grid highly non-uniform (too much actually), with density around the cluster point about 2-3 orders of magnitude higher than at the grid end points.

Usage

So how would we use the trained NN? Given a particular trade and set of market data, we now have a (hopefully) good enough approximation of our PDE engine's expected discretization error as a function of the two grid parameters, i.e. error = f(K, b). We can then proceed to find (K, b) that minimizes f. Normally f(spot, b) and f(strike, b) are convex with a unique minimum. So we could use a method like Brent to find the minimum. But since the NN approximation will be imperfect and may potentially in cases have some spurious local minimum forming somewhere, it is better to just sample the error at m equidistant values in the b-range. I used m = 15 here, first for K = strike and then for K = spot and picked the case with the overall lowest error. This means a total of 30 NN evaluations (inferences), each taking about 0.01ms on a modern CPU core (a few matrix multiplications), so the total prediction of the optimal grid parameters comes at about 0.3-0.4 milliseconds.

It is worth noting that while we obviously aim to approximate the error functional as closely as possible with the NN, in the end what we really care about is the location of the minimum and not the exact value. So while during training we evaluate the network performance using a metric like MAE or RMSE (note, we are talking about mean (NN approximation) error of the (PDE discretization) error here!), this is not our ultimate test of success. That would be whether the NN really choses the optimal grid construction for the particular trade and market data. To confirm that we would have to solve every case using all possible (K, b) combinations and calculate the actual error against the reference price, which is of course impractical.

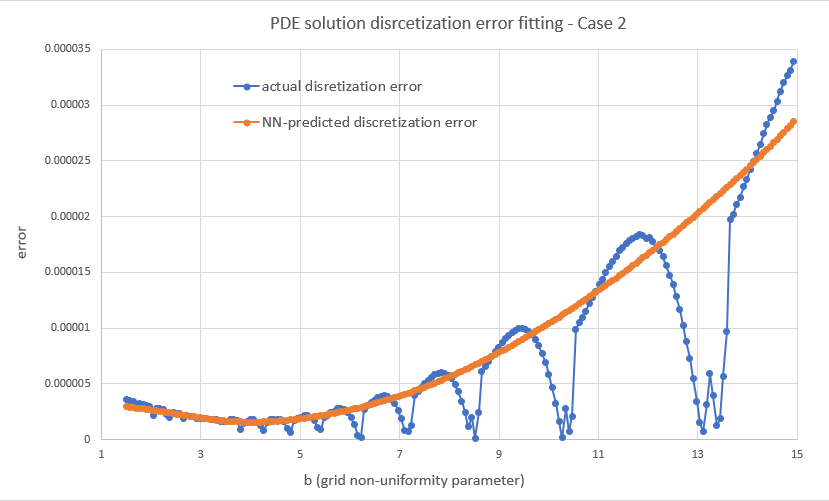
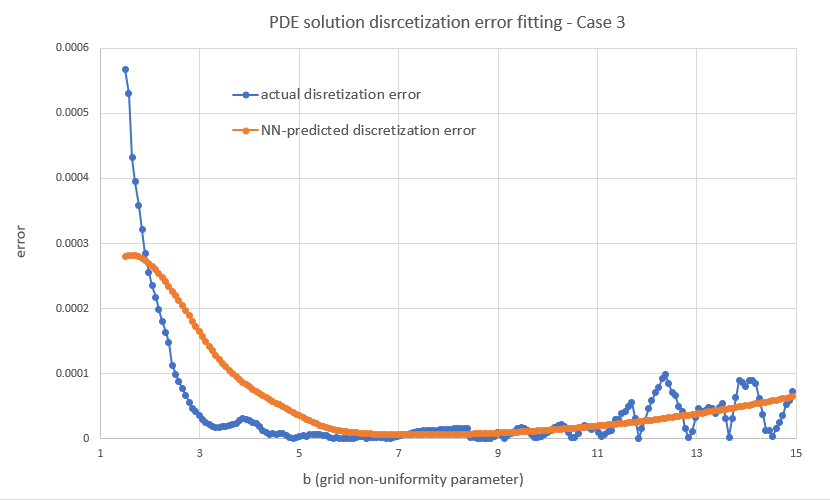
In reality the NN will miss the actual minimum in many cases. This is because f(K,b) can be a noisy function and the NN can only smooth it out, in which case it will miss the "fine detail" (more on this below). And even when it is smooth, the approximation may not be accurate enough to point to the correct minimum location. But it doesn't have to be, it just needs to be fairly close. That would be good enough since a close to optimal (K,b) will still beat some arbitrary choice and thus improve on the current strategy (likely some case-agnostic, static grid construction, i.e. using some fixed (K, b) for everything).

Results

Let's have a look first at some types of error behavior and the resulting NN fits to illustrate what I was referring to above, i.e. the error can be a smooth function of b like in case 1, but it may also look "weird" like the next two cases. As can be seen, the NN smooths out any "high fequency" detail, but correctly locates the level of b where the error would overall be lower. K = Strike here for all three cases.

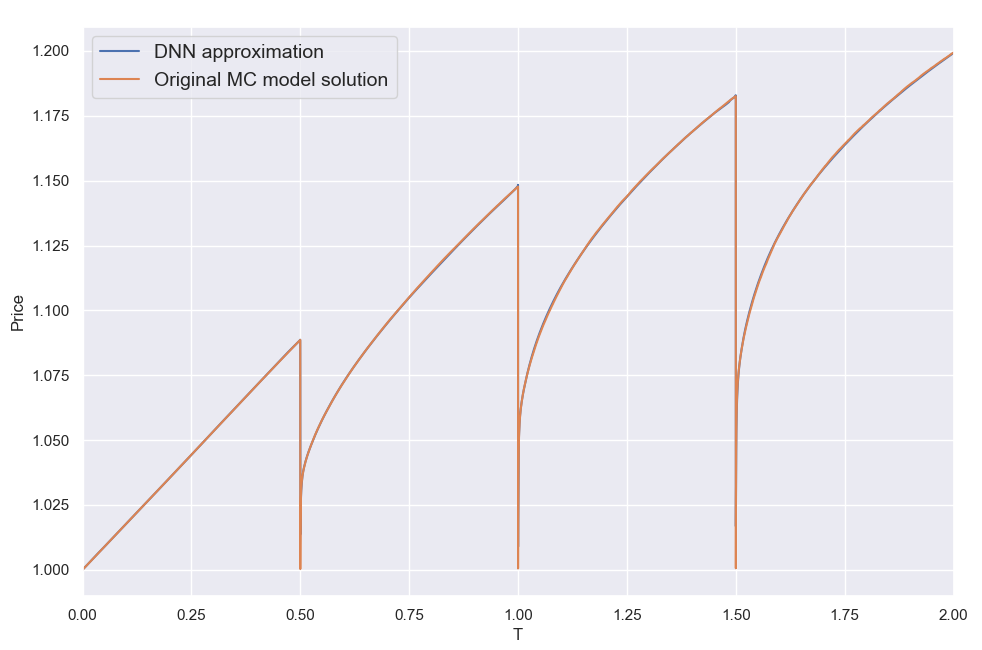
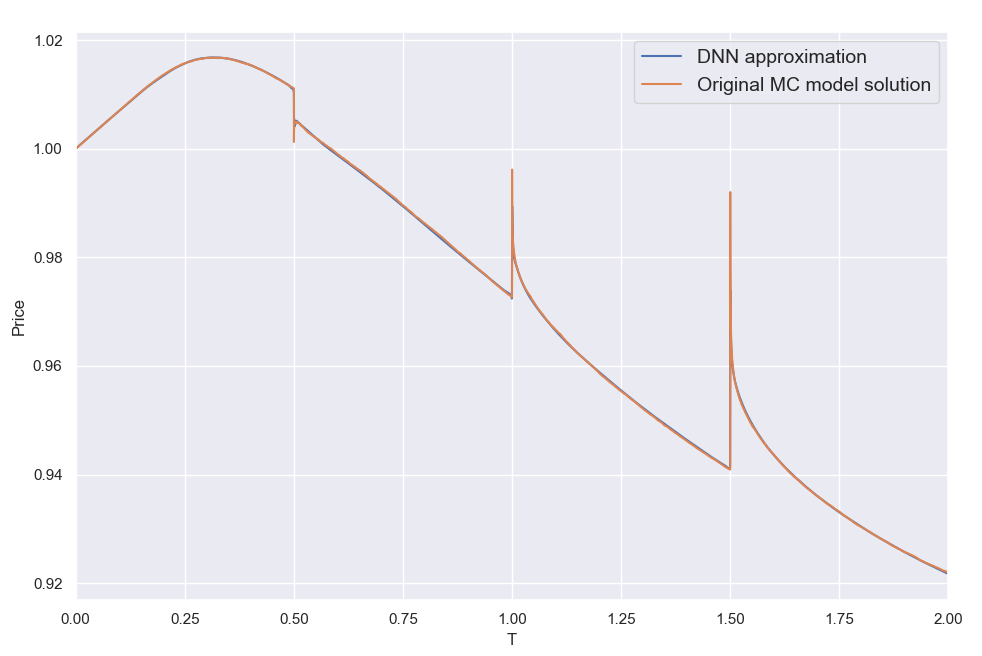
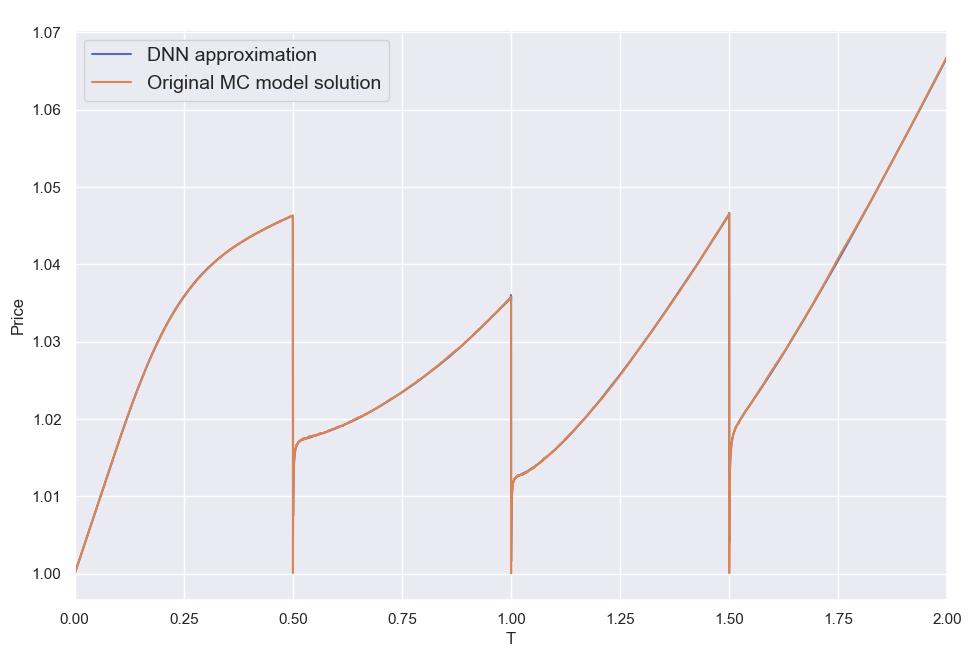
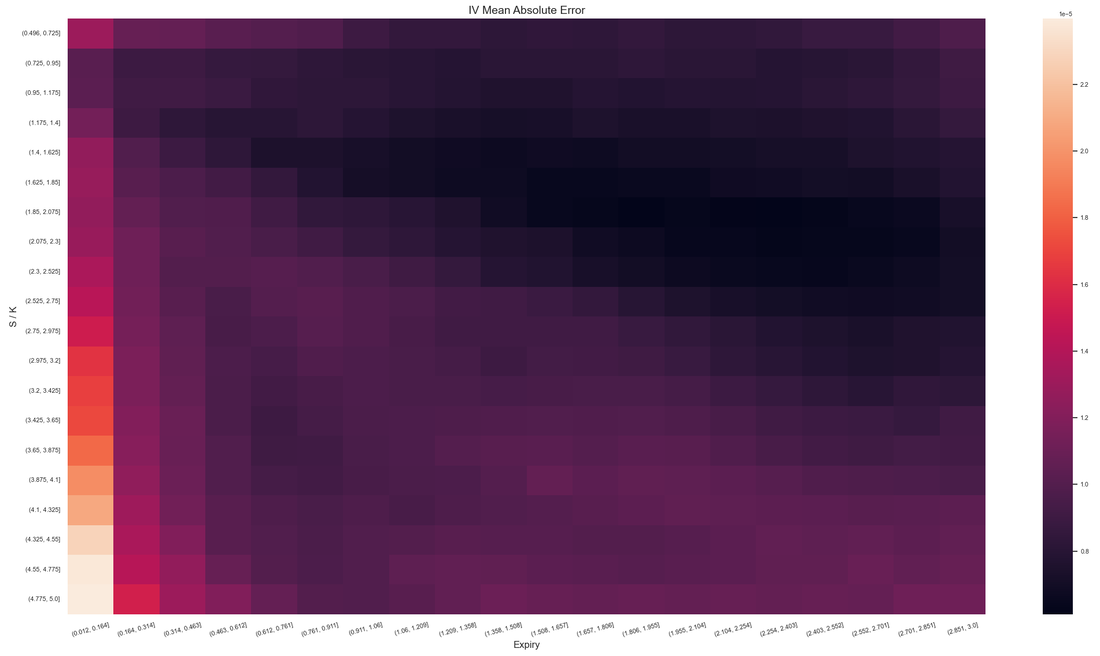
Overall I found that the NN is able to do a decent job of mapping the error to the inputs, despite its small size. My short testing (I am a freelance at this time with limited resources) indicates that both network and training set sizes used are already producing diminishing returns and in fact I got almost the same benefit training with just half the training set. With slightly larger NN sizes, visual inspection (like the ones above) for a few valuations I've looked into, showed improved fits but that did not translate to significant further improvement in the test below.

So finally to check if all this actually makes the TARF pricing significantly more accurate, I created a test set of 50K random trade & market data scenarios drawn from the same input ranges and distributions I used for the training and calculated the reference prices. I then calculated the prices with the working resolution of NS=200 using grids with various static (K, b) choices, a strike-clustered grid with dynamic NN-proposed optimal b and finally a fully NN-powered grid, with both the clustering focus and the value of b chosen by the NN dynamically (on a trade & market data basis). And then calculated the mean absolute error (MAE) across the test set for each of these strategies. The average pricing time with the working resolution (on a single CPU core) was 0.27 secs and the longest about 1.5 secs.

Table 1. Effect of different finite difference grid constructions on the accuracy of FX TARF valuations (mean absolute discretization error (for NS = 200) across 50,000 random trade & market data scenarios).

Grid focus (K)	b	Test set MAE
Strike	4	4.4E-06
	5	2.2E-06
	6	1.6E-06
	7	1.7E-06
	8	2.7E-06
	9	4.6E-06
Spot	4	3.2E-05
	5	2.6E-05
	6	3.8E-05
Strike	NN proposed	7.0E-07
NN proposed	NN proposed	4.0E-07
Heuristic	Heuristic	1.8E-06

As can be seen, using the strike as the grid focal point is generally the better "static "choice here, producing on average about an order of magnitude lower errors than when using the spot. The fixed value of b that minimizes the average error seems to be around b = 6. So if we were to just pick a simple grid construction strategy, this would be it, (K = Strike, b = 6). We then see that sticking with K = Strike and letting the NN pick the optimal value of b for each scenario, cuts the error by more than half. So pretty good I thought, but I knew that there are cases where K = Spot is a better choice. So could the NN successfully recognize such cases (or at least most of them) and switch to targeting the spot for those? The answer seems to be yes; letting the NN pick the optimal K as well, almost halves the error yet again.

Table 2. Comparison of the best static grid construction strategy with the optimal (NN-powered) strategy. Accuracy of FX TARF valuations (spatial discretization error for NS = 200) across 50,000 random trade & market data scenarios.

	(K=Strike, b=6)	NN proposed (K, b)
MAE	1.6E-06	4.0E-07
RMSE	2.3E-05	1.8E-06
Cases with error > 1.E-04	92	-
Maximum error	2.3E-03	8.6E-05

Not only that but it also drastically reduces large errors, the maximum error being < 1 b.p. while the best static grid strategy produces errors of up to 23 b.p. and has 92 scenarios priced with error > 1b.p. Or in terms of RMSE, the NN fine-tuning of the finite difference grid reduces the pricing RMSE by a factor of 12. Out of curiosity I also included in the test the (heuristic) construction I was using before and surprisingly it was a bit worse than the best simple construction. Oh well (it was a bit better at reducing large errors though).

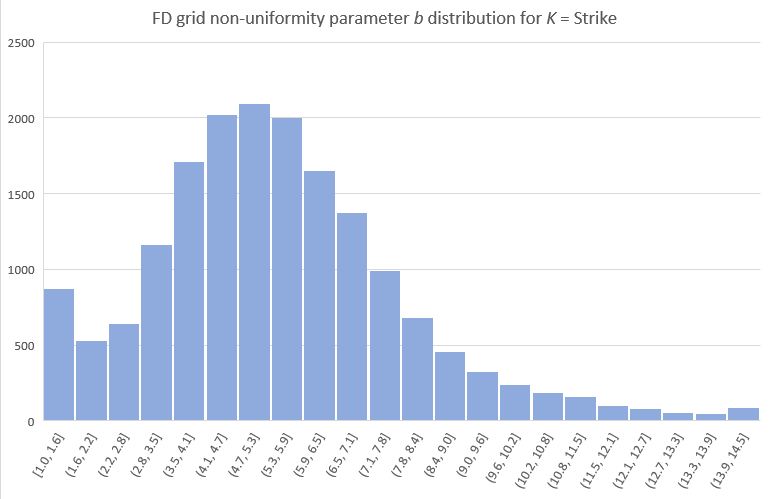
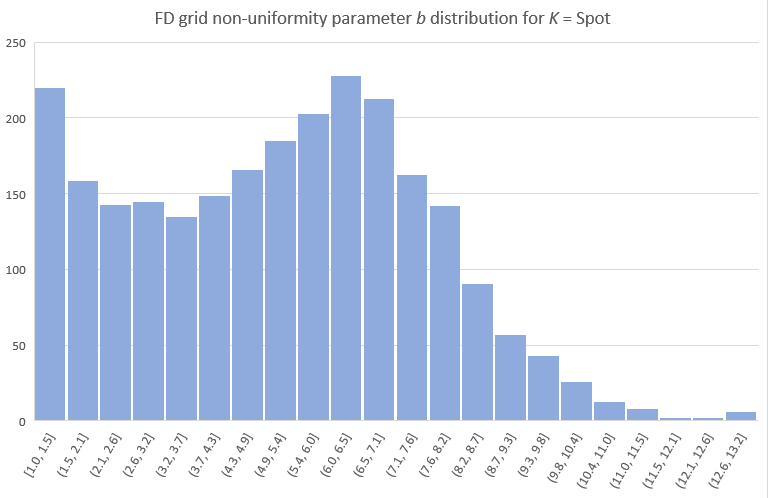
There is of course a lot of other interesting details (figures, tables) I could include, but I will stop here with the b distributions chosen by the NN for the test set, separately for K = Strike and K = Spot cases. Note that in some cases (mostly when the spot is the preferred grid focal point) a close to uniform grid is indeed optimal. The NN opted to use K = Spot for about 12% of the cases.

Before concluding I should probably stress that the NN is specifically trained to approximate the discretization error for a particular grid resolution (here NS=200) and if used to fine-tune the construction of a grid with a different number of spacings, the result will not in general be optimal. It will though very likely still improve on the best static construction. As a quick test I repriced the 50K test scenarios but this time with NS=100 grids, using the best static choice of (K = Strike, b = 6) plus the NN proposed (K, b) and calculated the errors like before. The NN-assisted construction still managed to cut the test MAE of the static construction to less than half (but not quite by a factor of 4 as it did for NS=200). To get the full benefit we would naturally need to train an NN specifically for NS=100.

Conclusion

So it turns out that training a small ANN to pick the optimal (trade & market data specific) finite difference grid construction for each pricing case, works and reduces discretization error levels significantly. This of course means that we could switch to smaller grid sizes, thus saving a lot of CPU time and resources.

Note that I went straight to applying this idea to a rather involved, "real world" PDE solver (with a less than straightforward grid generation), instead of trying it out first on a more "academic" test problem, say a simple barrier option. I may still do that out of curiosity.

Another potential variation would be to also include the resolution NS in the training, so that we can then be able to pick the best (NS, K, b) strategy for a desired error level.

Thanks for reading. If you found this idea interesting and decide to use it in your own research/work, please acknowledge this article and do get in touch, it would be nice to hear from you.

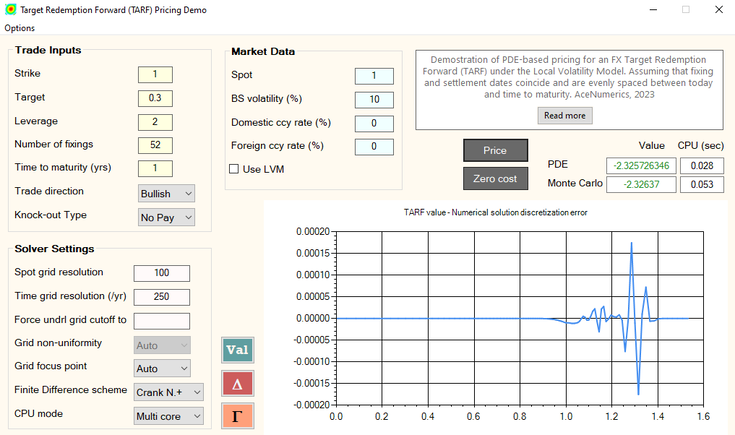
Finally, a demo TARF pricing GUI showcasing the overall speed of the PDE engine, and the effectiveness of the present "smart" grid construction in particular, is available for anyone interested.

References

[1] Y. Papadopoulos, A. Lewis, “A First Option Calibration of the GARCH Diffusion Model by a PDE Method.,” arXiv:1801.06141v1 [q-fin.CP], 2018.

0 Comments

How fast and accurate is your FX TARF pricing engine? Part 2: Local Volatility Model

2/16/2023

0 Comments

In my previous post I talked about fast and accurate pricing of FX Target Redemption Forwards (TARF's) using the PDE/FDM method. I did that in a flat volatility (Black Scholes) setting to briefly show that even in this simple case there can be a big difference in the performance of the TARF pricing engine, depending on how considerate one is, God (or the devil) is in the details.

Let me clarify that here I am obviously talking about accuracy in terms of the discretization error of the numerical solution, not the model error. Just like a Monte Carlo simulation needs as many optimizations (and iterations) as one can afford in order to get an acceptably converged result, the same holds for finite difference/element methods (FDM/FEM) - just replace iterations with grid/mesh size.

Setting up the PDE-based TARF pricing engine properly is not trivial in its implemention and testing its convergencge properties with flat volatility should be the first step. But of course in most applications a volatility model is necessary. So in this post I will just take the engine I built for the previous post and instead of flat volatility use a (space and time-dependent) local volatility function a la Dupire. This is a pretty easy upgrade. After all the engine's building blocks are a bunch of individual 1-D BS PDE solvers and all we need to do is allow the volatility to be a function, nothing else has to change. The only question is how much would this affect the computational efficiency of the engine. As it turns out, not much at all, provided your local volatility surface is not discontinuous and too wild (and you cache and re-use some coefficients between the solvers).

Since I do not currently have access to market data, my brief tests here will be based on a sample market implied volatility (IV) surface sourced from [1] :

Market data for USD/JPY from 11 June 2014 (spot = 102.00). Strikes implied assuming delta-neutral ATM type
	10 Put		25 Put		ATM		25 Call		10 Call		rates
Mat	vol	strike	vol	strike	vol	strike	vol	strike	vol	strike	dom	for
1M	6.08%	99.7800	5.76%	100.8834	5.53%	101.9929	5.63%	103.0908	5.81%	104.1573	-0.04%	0.20%
3M	7.08%	97.4668	6.53%	99.7695	6.15%	101.9921	6.20%	104.1550	6.44%	106.3104	0.07%	0.29%
6M	8.19%	94.7459	7.42%	98.4743	6.95%	102.0008	7.00%	105.4620	7.36%	109.0553	0.16%	0.40%
1Y	9.90%	90.0345	8.61%	96.3376	7.95%	102.0061	8.04%	107.6629	8.69%	114.0638	0.21%	0.52%

Local volatility surface construction

Without going into too much detail, the local volatility (LV) surface construction here is based on direct application of Dupire’s formula (using IV’s, not option values). To calculate the derivatives involved I calculated a fine grid of IV’s via interpolation of the market IV surface. For that I used Gaussian kernel interpolation in the delta dimension (later turned to strike scale). Such an approach by construction guarantees no arbitrage on single smiles and has an inherent extrapolation method (as suggested in [2]). In the time dimension I used cubic spline interpolation. For my sample IV surface this is just fine, but generally it could lead to calendar arbitrage and thus something more sophisticated would be used in practice to make sure of that. Either way, the LV surface construction is not the focus of this post, so I am assuming there is a good one available. Obviously the smoother the resulting surface, the smaller the negative effect on the finite difference scheme discretization error.

For the purpose of the present test I used 300 x 400 points in the strike and time dimension respectively (shown below). Most of the points in the strike dimension are placed around the spot. The above LV calibration procedure takes about 20 milliseconds. This surface is then interpolated (bi-)linearly by each solver to find the required local volatility function values on the pricing grid points. As for the quality of the calibration, using the same LV-enabled 1-D FD solvers making up the TARF pricing engine to price the market vanillas, produces an almost perfect fit in this case (IV RMSE about 0.001%).

Test results

So without further ado, let's look at the performance of the engine using local volatility. I will only use one test case for now (I might add more at a later edit), which my limited testing suggests is representative of the average performance. As can be seen, the average discretization error here is very low at about 0.16bp per unit notional (the maximum is 0.63bp) and the average CPU time is 60 milliseconds (timings exclude the LV calibration which as mentioned above takes about 20 milliseconds). It is obvious that the introduction of local volatility does not materially affect the efficiency of the PDE engine as showcased in the previous post for flat volatility (please read there for more details).

I will follow this up by introducing some sort of stochastic volatility as well, still aiming to keep the valuation time in the milliseconds (but we'll see about that).

Table 1. Performance of optimized PDE pricing engine for a Bullish TARF under the local volatility model (LV surface as shown above). Time to maturity = 1Y, number of fixings remaining = 52, target level = 15, leverage factor = 2, KO type = Full pay, spot = 102, domestic rate = 0.21%, foreign rate = 0.52%. The individual PDE solvers' space-time grid resolution is NS x NT = 200 x 350. The benchmark values were obtained with very high grid resolution and extrapolation and should be fully converged for the digits displayed.

strike	TARF Value	benchmark	abs(error)	CPU (sec)
94	17.772979	17.776078	3.1E-03	0.063
95	18.843706	18.843834	1.3E-04	0.069
96	17.691132	17.693761	2.6E-03	0.066
97	14.168072	14.168990	9.2E-04	0.057
98	5.400859	5.407167	6.3E-03	0.06
99	-13.002030	-13.003726	1.7E-03	0.06
100	-46.862257	-46.860844	1.4E-03	0.06
101	-99.130065	-99.131584	1.5E-03	0.06
102	-163.481890	-163.485062	3.2E-03	0.06
103	-235.729239	-235.728137	1.1E-03	0.06
104	-314.541043	-314.540662	3.8E-04	0.063
105	-398.791243	-398.791119	1.2E-04	0.061
106	-487.453001	-487.451061	1.9E-03	0.06
107	-579.580102	-579.579445	6.6E-04	0.06
108	-674.364545	-674.363590	9.5E-04	0.051
109	-771.158197	-771.157111	1.1E-03	0.049
110	-869.474221	-869.472986	1.2E-03	0.049

References

[1] N. Langrené, G. Lee and Z. Zili, “Switching to non-affine stochastic volatility: A closed-form expansion for the Inverse Gamma model,” arXiv:1507.02847v2 [q-fin.CP], 2016.
[2] Hakala, J. and U. Wystup, Foreign Exchange Risk, Risk Books, 2002

0 Comments

How fast and accurate is your FX TARF pricing engine?

12/16/2022

0 Comments

Wanting to take my mind off the constant bad news on this planet, I've been looking for little challenges. Pleased with my recent 5K runs dropping to around 24min (I know real runners, it's poor), I thought I should match it with some sort of equivalent mental effort. And what better way to test your brain power, stamina and discipline, than getting an answer to a real-world problem that has a PDE representation and have that PDE solved numerically (wait what?!). Anyway, spurred on by a recent interview question that made me realize I had focused too much on my machine learning adventures and pushed previous knowledge too far back in memory, I decided to price a Target Redemption Forward (TARF) as efficiently as possible. This was also a weak link in at least one of the places I've worked; I am not sure of the exact model or numerical method used (though I do know it was not a full LSV model), but they were sure taking a long time to price, in cases more than 30 seconds.

The easy way to price these is of course via Monte Carlo simulation; it is simple to implement and straightforward to accommodate any added contract bells and whistles. But MC is slow and it's tough to get good Greeks out of it. There is of course another way.

Pricing TARF's the PDE way

The TARF contract consists of a series of periodic payments (e.g. weekly or monthly) up to some maturity, but the contract can end prematurely when/if on a particular fixing date the specified target is reached. A bullish TARF for instance defines a strike K (usually set below the spot S at the time of issue) and a leverage factor g. At every fixing date the holder makes a profit of (S - K) if S is above K and a loss of g (K - S) is S fixes below K (per unit of notional); profits accrue towards the target (but losses do not).

So the structure is knocked out when/if the accrued amount A reaches the target. This is a strong path dependency feature; but unlike accumulators where the knock out depends on the path of the spot itself (which is already part of the numerical solution), here we need to somehow involve A in the solution. We do that by adding A as an extra pseudo-dimension, discretized by a number of individual 1-D PDE solvers (for Black Scholes, local volatility (LV) model, or local regime switching). Each of these solvers corresponds to an A-level within the range of possible values (from zero to the target).

Solving backwards from maturity, we march the option value in time separately for each solver until we reach a fixing/settlement date (for simplicity here I assume that fixing and settlement dates coincide). There we have a jump condition that must be applied in order to continue solving. More specifically, for each S-grid point on each solver we determine the payment to be made based on the S value and the solver's A level. Adding positive payments to the solver's A, gives us the implied A level that corresponds to each S grid point of the solver just after (in normal time direction) the payment has been made. Given the implied A level we can find the option value there by interpolating from the solutions of the solvers whose A levels are nearest (which we have all marched up to that time point). We do that with say cubic interpolation. The (initial, or rather final) values with which we start solving again towards the next fixing date are then found by adding the payout to the previously interpolated option values.

That is the outline (by the way, this "auxiliary state variable" method can be seen in action when pricing Asian options within the old option pricer in this site). I will stick with the basics here (no volatility model) in order to show that even in this simple setting the implementation leaves enough room for one to come up with a great, or not so great pricing engine.

So each individual solver is solving the Black Scholes pricing PDE using the Crank Nicolson method with Rannacher time-stepping on a non-uniform S-grid that places more points near the strike. This standard building block is well-optimized and one can use it as per above to put together a basic implementation of the TARF pricing engine. I did this and the results while still better than MC, left a lot to be desired in my view. Let's just say that a basic implementation results in a solution that does not behave optimally (and a lot worse than it does for Asian options by the way). So I tried to find ways to improve things. And here I will just give an indication of how much one can improve. The details that make this possible will not be the subject of this short post, but if one really wants to know you can contact me (using the contact form or the email in this paper).

Test cases

Here I am showing a couple of the many tests I did that showcase the typical performance differential between an optimized and a "naive", basic implementation. The individual solvers used were identical (S-grid, boundary conditions, etc) in both engine implementations. I was aiming for an accuracy of about $ 10^{-4} $ and the time discretization error was smaller than that when NT = 500 time steps were used. I played a bit with the S resolution (NS) to this end. The spacing between the the A (S-t) planes was roughly the same as the average S-grid spacing in both implementations (though uniform for the basic and non-uniform for the optimized). Note that there are generally three ways of handling the settlement of the fixing that results in the target being reached, i.e. three knockout types. a) No pay: payment is not made, b) Capped pay: there is partial payment so as to "fill" the target exactly, c) Full pay: payment is made in full. All three are of course trivially accommodated by the method.

The plots below show the spatial discretization error for the part of the solution that is of interest (the actual solver S-grid extends further) and assuming the accrued amount today is zero, i.e. A = 0. This may mean we are pricing at the time of issue, or at some time during the lifetime of the contract (in which case target stands for "remaining target"). The error profile is obtained by comparing the solution to that from an optimized engine using NS = 6000 and NT = 500 (this has really, really low spatial discretization error, < $10^{-8}$ to be precise). One CPU (Ryzen 5900X) core was used for the timings shown, though if need be the method is easily parallelized. Code is written in C++ and compiled with gcc on Linux. Interest rates are zero.

First we look at a one year contract with weekly fixings/payments and volatility typical of many FX rates. The knockout type is no pay and the leverage factor is two. The optimized version achieves the desired accuracy in 0.09 seconds, while the basic version needs a lot higher spatial resolution and 5 seconds to come close to that.

And now a two year contract and high underlying volatility (more common to precious metals). The knockout type in the case is full pay and the leverage factor is one. In this setting the optimized engine's relative advantage is more pronounced, achieving the desired level of accuracy in 0.06 seconds while the basic engine really struggles here and fails to come close even with a spatial resolution ten times higher. The keen observer will notice the basic problem here immediately.

And the same in log scale:

In case it is not clear to all readers, the plots above show that with a single split-second PDE solution we get very low error valuations for the whole range of spot values. This is of course under Black Scholes, but the same level of efficiency should carry over with a volatility model. Thus if the model and/or volatility dynamic assumed allows it, a whole spot ladder calculation should be possible in less than a second.

By the way, if the aim is a single spot valuation, it is often (but not always) preferable to cluster the grid points around the current spot (typical for example when one solves the PDE in log space). In this case one can get higher efficiency still, i.e. same discretization error in even less CPU time.

Some benchmark valuations

While I am at it, why not post some highly accurate benchmark valuations ("benchmark" being a theme in this site). It may be difficult to believe (and in a way pointless, same way as making watches waterproof to depths no human can survive is pointless), but all digits provided should be correct. Perhaps if someone wants to perform basic sanity checks on their TARF pricing engine these can be of some help. So to be clear, assuming fixing and settlement dates coincide and are all dt = 1/52 yrs apart (say forcing an ACT/364 day count with no holidays affecting the weekly fixings dates), flattening the volatility surface and zeroing rates curves, should have you approaching the values below as you increase your pricing engine's resolution (or Monte Carlo iterations).

Table 1. Benchmark valuations for a bullish Target Redemption Forward (TARF) under Black Scholes. In all cases the strike K = 1 and both domestic and foreign rates are zero. The values were obtained with a highly optimized PDE-based pricing engine and all digits shown should be converged, except the last one which may be off by 1 or 2 points.

Case	T (yrs)	num. fixings	target	lev. factor	KO type	spot	BS vol	TARF value
1	1	52	0.3	2	No Pay	1.06	10%	-0.02096094
2	1	52	0.5	2	No Pay	1.06	10%	-0.017514630
3	1	52	0.7	2	No Pay	1.06	10%	0.035902523
4	1	52	0.3	2	No Pay	1.1	10%	0.235120763
5	1	52	0.3	2	Capped pay	1.1	10%	0.286424762
6	1	52	0.3	2	Full pay	1.1	10%	0.335294058
7	1	52	0.3	1	No Pay	1.03	10%	-0.29368756
8	1	52	0.3	1	No pay	1.1	20%	-0.01224772
9	1	52	0.7	1	No pay	1.1	20%	0.037345388
10	1	52	0.7	1	Full pay	1.1	20%	0.152792822
11	2	104	0.3	1	No pay	1.35	40%	0.059232579
12	2	104	0.5	1	No pay	1.35	40%	0.315294774
13	2	104	0.5	1	Full pay	1.1	40%	-3.81704655

I will try to follow this up with an update using some volatility model.

0 Comments

Neural Networks in quant finance for high accuracy approximations Second case study: Structured products pricing - Multi Barrier Reverse Convertible Autocallable (MBRCA) on worst-performing of 4 assets

1/28/2022

1 Comment

As promised in the previous post, I am going to present here some first results on using Deep Neural Networks (DNN's) for producing ultra fast (and accurate) approximations of complex structured product pricing models. That means: take the model currently used (whatever it may be) that is computationally expensive (Monte Carlo) and replace it with a lightning fast equivalent with the same (or maybe higher?) accuracy as that used in the production environment. As anticipated, this proved a more challenging and time-consuming undertaking than the stochastic volatility model calibration of the previous post. The end result though is still very satisfactory and has room for improvement given more resources. A surprise to me given the much higher dimensionality and discontinuous (in time) nature of the approximated (model pricing) function.

Since I do not currently have access to a proper production model (that could for example employ some Local Stochastic Volatility model for the underlying processes), I will use simple GBM. The number of free input parameters (dimensionality of the approximated function) is 28 (see below), which combined with the pricing discontinuities at the autocall dates still make for a very challenging problem. My experience so far (on training DNN's for simpler exotics) is that replacing GBM with a volatility model does not pose unsurmountable difficulties for the DNN. I am confident that similar (or higher) accuracy to the one showcased here can be achieved for the same MRBCA, at the expense of more (offline) effort in generating data and training the DNN.

The product class

The product class we are looking at (autocallable multi barrier reverse convertibles) is popular in the Swiss market. It is a structured product paying a guaranteed coupon throughout its lifetime with a complex barrier option embedded. The latter is contingent on the worst performing out of a basket of underlying assets. There is a down-and-in type continuously monitored barrier and an up-and-out discretely monitored one (at the autocall dates). The assets' performance (level) is measured as a percentage of their initial fixing values. Accordngly, the strike level K for the down-and-in payoff, the down-and-in barrier B and the early redemption (autocall) level A (the "up-and-out barrier") are quoted as percentages.

In short: The product pays the holder a guaranteed coupon throughout its lifetime (up to maturity or early redemption). If on any of the observation (autocall) dates the worst-performing asset level is above the early redemption level, the product expires immediately and the amount redeemed is 100% of the nominal value. If no early redemption event happens then at maturity :

If during the lifetime of the product the worst-performing asset level did not at any moment touch or cross the barrier level B, the amount redeemed is 100% of the nominal value.
If the worst-performing asset level did touch or cross the barrier level B at some point and its final fixing level is above the strike level K, the amount redeemed is again 100% of the nominal value.
If the worst-performing asset did touch or cross the barrier level B at some point and its final fixing level is below the strike level K, the amount redeemed is the percentage of the nominal equal to the worst-performing asset performance (ratio of its final to initial fixing level).

The specific product to be approximated

I am not going to attempt an all-encompassing DNN representation of any possible MRBCA structure, but rather focus the effort on particular subcategory. So what I am looking for is a pricing approximation for MRBCA's on the worst of 4 assets, with original maturity of 2Y and semi-annual coupon payment and autocall dates. Also assuming the product is struck at-the-money (i.e. the strike level K is 100%, the most usual case in practice) with an early redemption (autocall) level of also 100%, again typical in the market. The latter two could of course also be included as variable inputs in the approximation. This may well be possible while maintaining the same accuracy but I haven't tried it yet.

So the DNN approximation will be for the clean price of any such product (given the inputs described next) at any time after its inception, up to its maturity. Indeed in what follows, T denotes the time left to maturity.

28 model inputs - features for the DNN training

The asset level S (% of initial fixing), volatility vol and dividend yield d for each of the 4 underlying GBM processes.
Seven-point discount factor curve (1D, 1W, 1M, 3M, 6M, 1Y, 2Y).
Time left to maturity T (in years).
Barrier level B (% of initial fixings).
Coupon level Cpn (% p.a.).
Correlation matrix (six distinct entries).

The DNN is trained for wide ranges of its inputs to allow it to be used for a long time without the need for retraining. The approximation is only guaranteed to be good within the input ranges that it has been trained for. Those are shown below.

Operational parameter ranges
	Min	Max
S_i	20%	500%
vol_i	10%	40%
d_i	0	10%
T	0.001	2
r (disc. rates)	-2%	2.50%
B	40%	80%
Cpn	2% p.a.	20% p.a.
ρ	-55%	99%

Pricing model implementation

The original pricing model / function we aim to "mimic" is of course based on Monte Carlo simulation and was written in C++. I omitted things like date conventions and calendars for ease of implementation. The continuously monitored (American) down-and-in barrier feature is taken care of via the use of a probabilistic correction (Brownian Bridge). Given the assumed GBM processes, this not only perfectly eliminates any simulation bias, but also enables the use of large time-steps thus allowing for significant speedup in the generation of the training samples. The discount curve interpolation is based on cubic splines and auxiliary points. The simulation can be driven by either pseudo random numbers or quasi random sequences (Sobol). I chose the former for the generation of the training samples as it proved to be more beneficial for the learning ability of the DNN under my current setup.

Note that in contrast with the use case in the previous post, here the training output data (the MC prices) are noisy and of limited accuracy. Does this represent a big problem for the DNN's ability to learn from them? It turns out that the answer is not really.

DNN Training and validation

The DNN is trained by feeding it millions of [vector(inputs), price] pairs. This process in practice has to be repeated many times since there is no general formula for what works best in each case. The pricing accuracy of the training set samples does not have to be as high as the target accuracy. As it turns out the DNN has the ability to effectively smooth out the pricing data noise and come up with an accuracy that is higher than that on the individual prices it was trained on. Also the input space coverage does not have to be uniform as we may want for example to place more points where the solution changes rapidly in an effort to end up with a balanced error distribution.

When it comes to testing the resulting DNN approximation though we create a separate (out of sample) test set of highly accurate prices uniformly filling the input space. This is to say we don't weigh some areas of the solution (say near the barrier) more than others when we calculate the error metrics. We say this is the operational (inputs) range of the DNN and we provide (or at least aim to) similar accuracy everywhere within that range. So the test set is created by drawing random inputs from uniform distributions within their respective ranges. The one exception being the correlation matrices whose coefficients follow the distribution below. We then discard those matrices that include coefficients outside our target range of (-55% to 99%).

The overall accuracy achieved by the DNN is measured by the usual Mean Absolute Error (MAE) and Root Mean Square Error (RMSE) metrics. We can also look at the error distribution to get an idea of how good the approximation is. What we cannot easily do is say what lies far in the tails of that distribution, or in other words provide some sort of limit for the maximum possible error. In contrast to the traditional MC model, there is no theoretical confidence interval for the DNN error.

The MAE and RMSE are calculated against a reference test set of 65K MC prices, each generated using 32 million Sobol-driven paths (with Brownian Bridge construction). Such prices are found (when re-calculating a subset using 268 million Sobol paths) to have an accuracy of 4.e-6, which is well below the target accuracy (about 1.e-4, or 1 cent in a nominal of 100$). The inputs were generated again using (22-dimensional, correlations excluded) Sobol points, in an effort to best represent the space. The average model price for this test set is 0.874 (87.4%).

In order to try and get an idea for the worst-case errors I tested the DNN against a much bigger (but less accurate) test set of 16.7 million Sobol points.

DNN approximation performance

For the results presented here the DNN was trained on 80 million [vector(inputs), price] samples carefully chosen so as to ensure that error levels are as uniform as possible across the input space. At this training set size the convergence rate (error decrease with each doubling of training set size) was showing some signs of slowing down, but there was still room for improvement. Using a few hundred million samples would still be straightforward and would yield even better accuracy.

Still the overall quality of the approximation is excellent. The mean error is less than a cent and generally does not exceed 3 cents. The speed is as expected many orders of magnitude higher than an MC simulation with similar standard error (see below). The timings are for a single CPU core. Of course if GPU's are used instead the speed can still be improved significantly.


Deep Neural Network Pricing Performance
	MAE	6×10^-5
	RMSE	9×10^-5
	Maximum absolute error in 16.7M test samples	1.5×10^-2
	CPU time per price (1 core)	6×10^-6 secs

in order to get similar accuracy from the traditional MC model one needs about 400K antithetic paths. With the present implementation this takes about 0.35 secs on 1 CPU core, which is about 60000 times slower than the DNN. If the MC pricing employed some volatility model needing fine time steps, the speedup factor could easily be in the order of millions (the DNN speed would remain the same).

The MC model prices a lot of the samples with almost zero error. This is because for many of the random input parameter vectors the solution is basically deterministic and the product behaves either like a bond or is certain to be redeemed early.

By far the most challenging dimension in the 28-dimentional function we are approximating here is the time to expiry T. The (clean) product price can be discontinuous at the autocall dates, posing a torture test for any numerical method. This is illustrated below where I am plotting a few sample solutions across T (keeping all other input parameters constant). These "pathological" cases correspond to the random input parameter vectors that resulted in the worst DNN approximation errors among the 16.7 million reference set cases (top 5 worst errors). The MC price plots are based on 40000 valuation points using 132K Sobol-driven paths per valuation. It took about 10 mins to create each plot utilizing all 12 cores of a CPU . The corresponding 40000 DNN approximations took < 0.2sec on a single core.

Looking at these plots it comes as no great surprise that the DNN struggles here. Considering the vast variety of shapes the solution can take, it is nonetheless seriously impressive that the DNN can cope as well as it does overall. That said, the maximum errors above are about 1.5% (not quite visible, located within those ultra narrow dips a few hours from the auto-call dates), which is more than I would have been happy with. Still, for use in XVA type calculations and intraday portfolio valuation monitoring, the performance is more than adequate as is. For use in a production environment one would need to be even more stringent with ensuring the maximum errors do not exceed a certain threshold. When testing the DNN against the much smaller 65K reference set, the maximum error was an order of magnitude smaller (about 0.2%, or 20 cents). Looking at 100M cases may reveal an even worse case than the 1.5% error found in the 16.7M set. Nonetheless there are ways to identify and target the problematic areas of the input parameter space. I am thus confident the maximum errors can be brought down further together with the mean error metrics by increasing and further refining the synthetic training set.

In conclusion, we can say that the DNN has passed this second much more difficult test as well. There was never a doubt that the approximation accuracy increases with increasing training data. The question in my mind was rather "is the sufficient amount of training (for the DNN to produce a worthy replacement of the traditional MC and PDE-based pricing) practical in terms of time and cost"? Given the experience gathered so far I would say the answer is yes. The present results were achieved mainly on a top spec desktop with only limited use of cloud resources. Approximating fully fledged models incorporating local and/or stochastic volatility will require more computational power, but the offline effort would still correspond to reasonable time and cost. To this end, a third post in this series would look at the case of FX TARF pricing under an LV or LSV model.

P.S. The results summarily presented in these last two posts are the culmination of a lot of work and experimentation that took the better part of a year and thousands of CPU/GPU hours.

1 Comment

Neural Networks in quant finance for high accuracy approximations First case study: Stochastic volatility model calibration (Heston)

11/5/2021

0 Comments

The last few years have seen increased interest in Machine Learning – Neural Networks (NN’s) in finance. Here I will focus specifically on the application of NN’s to function approximation, so basically derivatives pricing and consequently risk calculations. The goal is to either “turbo-boost” models/calculations that are already in production systems, or enable the use of alternative/better models that were previously not practical due to the high computational cost. I’ve been hearing claims of millions of times faster calculations and that the Universal Approximation Theorem guarantees that all functions can be approximated accurately by the simplest kind of net, provided enough training samples. But as usual the devil is in the details; like exactly how many training samples are we talking about to achieve a typical production system level of accuracy? I was wondering, what if to guarantee acceptable accuracy one would need impractically large training sets (and hence data generation and training times)? And never mind millions of times faster (perhaps more realistic for quantum computers when they arrive?), I would be satisfied with 100 or even 10 times faster, provided it was easy enough to implement and deploy.

There have been waves of renewed interest in NN's for decades, but their recent resurgence is in large part due to them been made more accessible via Python packages like TensorFlow and PyTorch that hide away the nitty gritty that would otherwise dishearten most of the recent users. So given the low barrier to entry and having been spurred on by a couple of people, I decided to check out this seemingly all-conquering method. Moreover, this seems like an engineering exercise; one needs to be willing to try a lot of different combinations of “hyperparameters”, use suitable training sample generation techniques and bring in experience/tricks from traditional methods, all with the aim to improve the end result. Not to mention "free" time and relatively cheap, sustainable electricity. That’s me then this year I thought.

I am not sure what is the state of adoption of such NN applications in finance right now. Looking at relevant papers, they all seem to be fairly recent and more the proof-of-concept type. What puzzles me in particular is the narrow input parameter range used to train the NN's on. Surely one would need more coverage than that in practice? Consequently there is talk that such (NN) models would need to be retrained from time to time when market parameters get out of the “pre-trained” range. Now I may be missing something here. First, I think it would be less confusing to call them "NN approximations" instead of "NN models" since they simply seek to reproduce the output of existing models. The application of NN’s in this context really produces a kind of look-up table to interpolate from. As for the limited range of parameters that is usually chosen for training in the relevant literature, I imagine it has to do with the fact that the resulting approximation's accuracy is of course higher like that. But this does not give me any assurance that the method would be suitable for real-world use, where one would need quite a bit higher accuracy still than what I have seen so far and also wider input ranges.

So I decided I want hard answers: can I approximate a model (function) in the whole (well almost) of its practically useful parameter space so that there’s no need to retrain it, like never (unless the original is changed of course)? To this aim I chose a volatility model calibration exercise as my first case study. Which is convenient because I had worked on this before. Note that a benefit of the NN approach (if it turns out they do the job well) is that one could make the calibration of any model super-fast, and thus enable such models as alternatives to the likes of Heston and SABR. The latter are popular exactly because they have fast analytical solutions or approximations that make calibration to market vanillas possible in practical timescales.

To demonstrate said benefit, the logical thing to do here would be to come up with a turbo-charged version of the non-affine model demo calibrator. The PDE method used in there to solve for vanilla prices under those models is highly optimized and could be used to generate the required millions of training samples for the NN in a reasonable amount of time. To keep things familiar though and save some time, I will just try this on the Heston model whose training samples can be generated a bit faster still (I used QLib’s implementation for this). If someone is interested in a high accuracy, production-quality robust calibration routine of any other volatility model, feel free to get in touch to discuss.

Like I said above, the trained parameter range is much wider than anything I’ve seen published so far but kind of arbitrary. I chose it to cover the wide moneyness (S/K) range represented by the 246 SPX option chain A from [1]. Time to maturity ranges from a few days up to 3 years. The model parameters should cover most markets. The network has about 750,000 trainable parameters, which may be too many, but one does not know beforehand what accuracy can be achieved with what architecture. It is possible that a smaller (and thus even faster) network can give acceptable results. 32 million optimally placed training samples were used. I favored accuracy over speed here, if anything to see just how accurate the NN approximation can practically get. But also because higher accuracy minimizes the chance of the optimizer converging to different locales (apparent local minima) depending on the starting parameter vector (see [3] for more on this).

Overall this is a vanilla calibration set-up, where a standard optimizer (Levenberg-Marquardt) is used to minimize the root mean square error between the market and model IV's, with the latter provided by the (Deep) NN approximation. There are other more specialized approaches involving NN's designed specifically for the calibration exercise, see for example the nice paper by Horvath et al. [4]. But I tried to keep things simple here. So how does it perform then?

Neural Network Approximation specification
	Operational parameter ranges
		min	max
	S/K	0.5	5
	T	0.015	3
	r	-0.02	0.1
	d	0	0.1
	v₀	0.002	0.5
	v̅	0.005	0.25
	κ	1	20
	ξ	0.1	10
	ρ	-0.95	0.1
	Performance
	Mean Absolute IV Error		9.3×10^-6

The mean absolute error is about 1.e−3 implied volatility percentage points (i.e. 0.1 implied volatility basis points).

The maximum error over a test set of 2 million (out of sample) random points was 5 IV basis points but that is in an area of the parameter hypercube of no interest in practice. For example on the moneyness - expiration plane, the error distribution looks like this:

Obviously for individual use cases the NN specification would be customized for a particular market, thus yielding even better accuracy and/or higher speed. Either way I think this is a pretty satisfactory result and it can be improved upon further if one allows for more resources.

In terms of calibration then, how does that IV accuracy translate to predicted model parameter accuracy? I will use real-world market data that I had used before to test my PDE-based calibrator; the two SPX option chains from [1] and the DAX chain from [2]. As can be seen in Table 1, the calibration is very accurate and takes a fraction of a second. In practice one would use the last result as the starting point which should help the optimizer converge faster still.

For those who need hard evidence that this actually works as advertised, there's the self-contained console app demo below to download. The options data files for the 3 test chains are included. The calibrator always starts from the same parameter vector (see Table 1) and uses only the CPU to keep things simple and facilitate comparisons with traditional methods. And I have also included a smaller, only slightly less accurate on average NN approximation that is more than double as fast still.

Neural Network based Heston model calibrator demo v1.1 (Windows)

Table 1. Model parameters calibrated to real market data: comparison between NN-based and exact (using Qlib at maximum accuracy settings) calibration . The starting parameter vector is (0.1, 0.1, 5, 2, -0.7).

	SPX Chain A from [1] (246 options)			SPX Chain B from [1] (68 options)			DAX Chain from [2] (102 options)
	Exact	NN	error	Exact	NN	error	Exact	NN	error
v0	0.007316	0.007315	(0.01%)	0.04575	0.04576	(0.02%)	0.1964	0.1964	(0.00%)
v̅	0.03608	0.03608	(0.00%)	0.06862	0.06862	(0.00%)	0.07441	0.07440	(0.01%)
k	6.794	6.794	(0.00%)	4.906	4.903	(0.06%)	15.78	15.80	(0.13%)
x	2.044	2.044	(0.00%)	1.526	1.525	(0.07%)	3.354	3.356	(0.06%)
r	-0.7184	-0.7184	(0.00%)	-0.7128	-0.7129	-(0.01%)	-0.5118	-0.5118	(0.00%)
IV RMSE (b.p.)	128.24	128.23	0.01	101.35	101.37	0.02	131.72	131.72	0.00
CPU time		0.55 s			0.16 s			0.26 s

So to conclude, it is fair to say that the NN (or should I say Machine Learning) approach passed the first real test I threw at it with relative ease. Yes, one needs to invest time to get a feeling of what works and come up with ways to optimize since this is basically an engineering problem. But the results show that at least in this case one can get all the accuracy practically needed in a reasonable amount of (offline) time and resources.

Finally let's briefly mention here the two main perceived issues with this approach: How does one guarantee accuracy everywhere in the input parameter hyperspace (i.e. looking at the tails of the error distribution)? I agree this is an issue but there are ways to increase confidence, especially in relatively simple cases like the one here. The other is lack of transparency and/or interpretability.

COMING UP NEXT: The follow-up post will feature a much more ambitious test: accurate pricing approximation of Barrier Reverse Convertible Autocallables on 4 underlyings. The accuracy demands will be somewhat lower (reflecting the original Monte Carlo pricing), but the training data will be noisy and the dimensionality much higher. I anticipate significant difficulties in guaranteeing an acceptable level of accuracy everywhere given the rapidly changing price function near the barrier for small times to expiry and especially the true temporal discontinuities on the auto-call dates. Can the NN deliver? Stay tuned to find out!

References

[1] Y. Papadopoulos, A. Lewis (2018), “A First Option Calibration of the GARCH Diffusion Model by a PDE Method.”, arXiv:1801.06141v1 [q-fin.CP].
[2] Kangro, R., Parna, K., and Sepp, A., (2004), “Pricing European Style Options under Jump Diffusion Processes with Stochastic Volatility: Applications of Fourier Transform,” Acta et Commentationes Universitatis Tartuensis de Mathematica 8, p. 123-133.
[3] Cui, Y., del Bano Rollin, S., Germano, G. (2017), "Full and fast calibration of the Heston stochastic volatility model", European Journal of Operational Research, 263(2), p. 625–638
[4] Horvath, B., Muguruza, A., Tomas, M. (2019). "Deep learning volatility.", arXiv:1901.09647v2 [q-fin.MF]

0 Comments

Fast option calibration: more non-affine stochastic volatility models.

2/27/2018

0 Comments

When it comes to stochastic volatility (SV) models (whether in their pure form, or typically in combination with local volatility and/or jumps), their adoption in practice has been largely driven by whether they offer an "analytical" solution for vanilla options. The popularity of the Heston model probably best exemplifies this. When such a solution doesn't exist, calibration (to the vanilla option market) is considered more difficult and time consuming. But what are the chances that a model that happens to have a (semi-) analytical solution is also the best for the job? It could happen of course, but obviously this isn't the right criterion when choosing the model. Another model may well fit the market's implied volatility surfaces better and describe its dynamics more realistically.

In my last couple of posts I spoke about how a fairly simple PDE / finite differences approach can actually enable fast and robust option calibrations of non-affine SV models. I also posted a little console app that demonstrates the approach for the GARCH diffusion model. I have since played around with that app a little more, so here I'm giving a second version that can calibrate the following 5 non-affine SV models (plus Heston for comparison).

For the GARCH diffusion or power-law model (and the PDE pricing engine used for all the models implemented in this demo) see [1]. For the Inverse Gamma (aka "Bloomberg") model see for example [2]. The XGBM model was suggested to me by Alan Lewis, who has been working on an exact solution for it (to be published soon). Here pricing is done via the PDE engine. The ACE-X1 model is one of the models I've tried calibrating, which seems to be doing a very good job in various market conditions. All the above models calibrate to a variance (or volatility) process that is arguably more realistic than that of the Heston model (which when calibrated, very often has zero as its most probable value in the long-run).

Non-affine SV Option Calibrator demo (Windows)

Please bear in mind that the above demo is just that, i.e. not production-level. In [1] the PDE engine was developed just for the GARCH diffusion model and Excel was used for the optimization. I then quickly coupled the code with a Levenberg-Marquardt implementation and adjusted the PDE engine for the other models without much testing (or specific optimizations). That said, it works pretty well in general, with calibration times ranging from a few seconds up to a minute. It offers three speed / accuracy settings, but even with the fastest setting calibrations should be more accurate (and much faster) than any Monte-Carlo based implementation. A production version for a chosen model would be many times faster still. Note that you will also need to download the VC++ Redistributable for VS2013. The 64-bit version (which is a little faster) also requires the installation of Intel's MKL library. The demo is free but please acknowledge if you use it and do share your findings.

EDIT April 2020: After downloading and running this on my new Windows 10 laptop I saw that the console was not displaying the inputs as intended (it was empty). To get around this please right click on the top of the console window, then click on Properties and there check "Use legacy console". Then close the console and re-launch.

As a small teaser, here's the performance of these models (in terms of IV-RMSE, recalibrated every day) for SPX options during two months at the height of the 2008 crisis. Please note that I used option data (from www.math.ku.dk/~rolf/Svend/) which include options +- 30% in moneyness only. Expirations range from 1M to 3Y. Including further out-of-the-money options does change the relative performance of the models. As does picking a different market period. That being said, my tests so far show that the considered models produce better IV fits than Heston in most cases, as well as representing arguably more realistic dynamics. Therefore they seem to be better candidates to be combined with local volatility and/or jumps than Heston.

	Heston	GARCH	Power_law_0.8	ACE-X1	I-Ga	XGBM
average IV-RMSE	0.91%	0.81%	0.82%	0.66%	0.73%	0.45%

References

[1] Y. Papadopoulos, A. Lewis, “A First Option Calibration of the GARCH Diffusion Model by a PDE Method.,” arXiv:1801.06141v1 [q-fin.CP], 2018.
[2] N. Langrené, G. Lee and Z. Zili, “Switching to non-affine stochastic volatility: A closed-form expansion for the Inverse Gamma model,” arXiv:1507.02847v2 [q-fin.CP], 2016.

0 Comments

Option calibration of non-affine stochastic volatility models. Case study: The GARCH diffusion model.

1/21/2018

1 Comment

My last two posts were really about just a couple of the many experiments I did as part of a project I had been working on. The aim was to design a method for efficient option calibrations of the GARCH diffusion stochastic volatility model. This (and other non-affine) models are usually thought of as impractical for implied (risk-neutral) calibrations because they lack fast semi-analytic (characteristic function-based) vanilla option pricing formulas. But using an efficient PDE-based solver may be an alternative worth looking at. It may prove fast enough to be used for practical calibrations, or at the very least provide insight on the overall performance of (non-affine) models that have seen increased interest in recent years. Besides, analytical tractability definitely shouldn't the main criterion for choosing a model.

For those interested there's now a detailed report of this joint collaboration with Alan Lewis on the arXiv: A First Option Calibration of the GARCH Diffusion Model by a PDE Method. Alan's blog can be found here.

GARCH Diffusion Option Calibrator demo (Windows)

EDIT: For the results reported in the paper, Excel's solver was used for the optimization. I've now quickly plugged the PDE engine into M. Lourakis' Levenberg-Marquardt implementation (levmar) and built a basic demo so that perhaps people can try to calibrate the model to their data. It doesn't offer many options, just a fast / accurate switch. The fast option is typically plenty accurate as well. So, if there's some dataset you may have used for calibrating say the Heston model, it would be interesting to see how will the corresponding GARCH diffusion fit compare. Irrespective of the fit, GARCH diffusion is arguably a preferable model, not least because it typically implies more plausible dynamics than Heston. Does this also translate to more stable parameters on recalibrations? Are the fitted (Q-measure) parameters closer to those obtained from the real (P-measure) world? If the answers to the above questions are mostly positive, then coupling the model with local volatility and/or jumps could give a better practical solution than what the industry uses today. (Of course one could just as easily do that with the optimal-p model instead of GARCH diffusion, as demonstrated in my previous post.) Something for the near future.

If you do download the calibrator and use it on your data, please do share your findings (or any problems you may encounter), either by leaving a comment below, or by sending me an email. As a bonus, I've also included the option to calibrate another (never previously calibrated) non-affine model, the general power-law model with p = 0.8 (sitting between Heston and GARCH diffusion, see [1]).

Note that (unless you have Visual Studio 2013 installed) you will also need to download the VC++ Redistributable for VS2013. The 64-bit version (which is a little faster) also requires the installation of Intel's MKL library.

EDIT April 2020: After downloading and running this on my new Windows 10 laptop I saw that the console was not displaying the inputs as intended (it was empty). To get around this please right click on the top of the console window, then click on Properties and there check "Use legacy console". Then close the console and re-launch.

I am also including in the download a sample dataset I found in [2] (DAX index IV surface from 2002), so that you can readily test the calibrator. I used it to calibrate both Heston (also calibrated in [2], together with many other affine models) and GARCH diffusion. In contrast to the two datasets we used in the paper, in this case GARCH diffusion (RMSE = 1.14%) "beats" Heston (RMSE = 1.32%). This calibration takes about 5 secs. This is faster than the times we report on the paper and the reason is that the data we considered there include some very far out-of-the-money options that slow things down as they require higher resolution. The Levenberg-Marquardt algo is also typically faster than Excel's solver for this problem. It is also "customizable", in the sense that one can adjust the grid resolution during the calibration based on the changing (converging) parameter vector. Still, this version is missing a further optimization that I haven't implemented yet, that I expect to reduce the time further by a factor of 2-3.

The fitted parameters are:
GARCH: v0 = 0.1724, vBar = 0.0933, kappa = 7.644, xi = 7.096, rho = -0.5224.
Heston: v0 = 0.1964, vBar = 0.0744, kappa = 15.78, xi = 3.354, rho = -0.5118.
Note that both models capture the short-term smile/skew pretty well (aided by the large fitted xi's, aka vol-of-vols), but then result in a skew that decays (flattens) too fast for the longer expirations.

References

[1] Y. Papadopoulos, A. Lewis, “A First Option Calibration of the GARCH Diffusion Model by a PDE Method.,” arXiv:1801.06141v1 [q-fin.CP], 2018.
[2] Kangro, R., Parna, K., and Sepp, A., (2004), “Pricing European Style Options under Jump Diffusion Processes with Stochastic Volatility: Applications of Fourier Transform,” Acta et Commentationes Universitatis Tartuensis de Mathematica 8, 123-133.

1 Comment

The ROD stochastic volatility 'model'

12/11/2017

1 Comment

It well known that pure diffusion stochastic volatility (SV) models like Heston struggle to reproduce the steep smiles observed in the implied volatilities of short-term index options. Trying to remedy this deficiency, the usual approach is to introduce jumps. More recently and as an alternative to jumps, some researchers have been experimenting with the use of fractional Brownian motion as the driver for the volatility process. Volatility they say is rough. Such a model is apparently able to capture steep short-term smiles. Basically both these approaches assume that pure diffusion models are not up to the task so alternatives are needed.

However, other voices suggest that this isn't necessarily true and that models of the Heston type have simply not been used to their full potential. They say why use a deterministic starting point $v_0$ for the variance when the process is really hidden and stochastic? Instead, they propose to give such traditional SV models a "hot start", that is assume that the variance today is given by some distribution and not a fixed value. Mechkov [1] shows that when the Heston model is used like that it is indeed capable of "exploding" smiles as expiries tend to zero. Jacquier & Shi [2] present a study of the effect of the assumed initial distribution type.

The idea seems elegant and it's the kind of "trick" I like, because it's simple to apply to an existing solver so it doesn't hurt trying it out. And it gets particularly straightforward when the option price is found through a PDE solution. Then the solution is automatically returned for the whole range of possible initial variance values (corresponding to the finite difference grid in the v-direction). So all one has to do in order to find the "hot-started" option price at some asset spot $ S_0 $ is average the solution across the $ S=S_0 $ grid line using the assumed distribution. Very simple. Of course we have to choose the initial distribution family-type and then we can find the specific parameters of that distribution that best fit our data. How? We can include them in the calibration.

So here I'm going to try this out on a calibration to a chain of SPX options to see what it does. But why limit ourselves to Heston? Because it has a fast semi-analytical solution for vanillas you say. I say I can use a fast and accurate PDE solver instead, like the one I briefly tested in my previous post. Furthermore, is there any reason to believe that a square root diffusion specification for the variance should fit the market, or describe its dynamics better? Maybe linear diffusion could work best, or something in between. The PDE solver allows us to use any variance power p for the diffusion coefficient between 0.5 and 1, so why not let the calibration decide the optimal p, together with the initial distribution parameters and the other model parameters. Let's call this the Randomized Optimal Diffusion (ROD) SV "model".

Sounds complicated? It actually worked on the first try. Here's what I got for the end of Q1 2017. Just using the PDE engine and Excel's solver for the optimization. The calibration involved 262 options of 9 different expiries ranging from 1W to 3Y and took a few minutes to complete. If one restricts the calibration to mainly short-term expiries then better results are obtained, but I wanted to see the overall fit when very short and long expiries are fitted simultaneously. I am also showing how the plain Heston model fares. Which on the face of it is not bad, apart for the very short (1W) smile. Visually what it does is try to "wiggle its way" into matching the short-term smiles. The wiggle seems perfectly set up for the 3W smile, but then it turns out excessive for the other expiries. The ROD model on the other hand avoids excessive "wiggling" and still manages to capture the steep smiles of the short expiries pretty well. The optimal model power p here was found to be 0.84. This is responsible for the less wiggly behavior compared to Heston's p = 0.5. The ability to capture the steep short-term smiles is solely due to the hot-start. And it's the hot-start that "allows" for that higher p. To put it another way, by making it easy to fit the short-term smiles it then allows for a better fit for all expiries. The overall RMSE for the Heston model is 1.56% while for the ROD model it's 0.86%.

But the RMSE only tells half the story. The Feller ratio corresponding to Heston's fitted parameters is 0.09, which basically means that the by far most probable (risk-neutral) long-run volatility value is zero. In other words, the assumed volatility distribution is not plausible. The randomization idea is neither without any issues, despite the impressive improvement in fit. The optimizer calibrated to a correlation coefficient of -1 for this experiment, which seems extreme and not quite realistic.

By the way, this experiment is part of some research I've been doing in collaboration with Alan Lewis, the results of which will be available/published soon.

References

[1] Serguei Mechkov. 'Hot-Start' Initialization of the Heston Model.
[2] Antoine Jacquier, Fangwei Shi. The randomized Heston model.

1 Comment

How efficient is your Heston (or similar) PDE solver?

12/4/2017

1 Comment

Last year I wrote an overly long post comparing the performance of an old Heston PDE solver of mine with those available in QuantLib. I was surprised to see that despite not using ADI techniques, it still seemed to produce very accurate solutions in a few seconds, just like QuantLib's ADI solvers. Published papers from the last 10 years or so also indicate that the calculation time in order to get high-accuracy prices from this 2D PDE is a few seconds give or take (on 5-10 yrs old CPUs). I've even seen a paper from last year presenting a "very efficient", state-of-the-art finite element method that gets Heston vanilla prices in 30 (!) seconds.
This year though I've worked a lot more on such solvers and I now realise that those run times are clearly not what one should be expecting, nor aim for with (fine-tuned) implementations. So just how fast should your numerical solver of the Heston (or similar) PDE be? What kind of run time should be expected for high-accuracy solutions? The answer is: a few milliseconds. Back in that Aug 2016 post I used some test cases from various papers and I'll use those again here, all puts:

	κ	η	σ	ρ	r_d	r_f	T	K	ν_o
Case 0	5	0.16	0.9	0.1	0.1	0	0.25	10	0.0625
Case 1	1.5	0.04	0.3	-0.9	0.025	0	1	100	0.0625
Case 2	3	0.12	0.04	0.6	0.01	0.04	1	100	0.09
Case 3	0.6067	0.0707	0.2928	-0.7571	0.03	0	3	100	0.0625
Case 4	2.5	0.06	0.5	-0.1	0.0507	0.0469	0.25	100	0.0625
Case 5	3	0.04	0.01	-0.7	0.05	0	0.25	100	0.09

My current "state-of-the-art" solver uses second-order spatial discretization and the Hundsdorfer-Verwer ADI scheme. For the results below I used the solver "as is", so no fine-tuning for each case, everything (grid construction) decided automatically by the solver. In order to give an idea of the accuracy achieved overall for each case I plot the solution error in the asset direction (so across the moneyness spectrum). The plots are cut-off where the option value becomes too small, the actual grids used by the solver extend further to the right. I am showing results for two different grid resolutions (NS x NV x NT), grid A (60 x 40 x 30) and grid B (100 x 60 x 50). The timings were taken on an i7-920 PC from 2009 in single-threaded mode. Obviously one can expect at least double single-thread speed from a modern high-spec machine. (ADI can be parallelized as well with almost no extra effort, with a parallel efficiency of about 80% achieved using basic OpenMP directives). The errors in each case are calculated by comparing with the exact (semi-analytic) values obtained using QuantLib at the highest precision. Note that I am using the relative errors which are harder to bring down as the option value tends to zero. But when one wants to use the PDE solver as the pricing engine for a calibration, then it is important to price far out-of-the-money options with low relative errors in order to get accurate implied volatilities and properly capture any smile behavior. The present solver can indeed be used to calibrate the Heston model (or any other model in this family) accurately in less than a minute and in many cases in just a few seconds.

So, if you have a Heston PDE solver then this is an efficiency reference you can use to benchmark against. Price the 6 options above and compare error plots and timings with those below. Let me know what you get. If you're getting larger errors than I do with the above resolutions, I'll tell you why that is!

There is of course another important quality for a PDE solver, robustness. The scheme I used here (H-V) is fairly robust, but can still produce some spurious oscillations when one uses too low NT/NS. I may expand this post testing other schemes in the near future.

1 Comment

<<Previous

How fast and accurate is your FX TARF pricing engine? (Part 4) Download this demo to compare notes!

How fast and accurate is your FX TARF pricing engine? Part 3: I asked ChatGPT to optimize the finite difference engine (and it worked)

The main idea:

The Neural Network

Usage

Results

Conclusion

References

How fast and accurate is your FX TARF pricing engine? Part 2: Local Volatility Model

Local volatility surface construction

Test results

References

How fast and accurate is your FX TARF pricing engine?

Pricing TARF's the PDE way

Test cases

Some benchmark valuations

Neural Networks in quant finance for high accuracy approximations Second case study: Structured products pricing - Multi Barrier Reverse Convertible Autocallable (MBRCA) on worst-performing of 4 assets

The product class

The specific product to be approximated

28 model inputs - features for the DNN training

Pricing model implementation

DNN Training and validation

DNN approximation performance

Neural Networks in quant finance for high accuracy approximations First case study: Stochastic volatility model calibration (Heston)

References

Fast option calibration: more non-affine stochastic volatility models.

References

Option calibration of non-affine stochastic volatility models. Case study: The GARCH diffusion model.

References

The ROD stochastic volatility 'model'

References

How efficient is your Heston (or similar) PDE solver?

Author

Archives

Categories