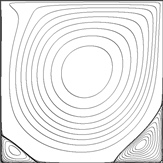
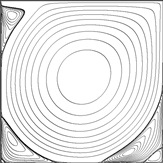
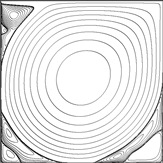
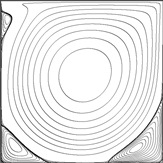
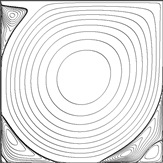
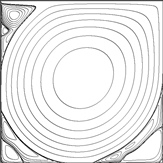
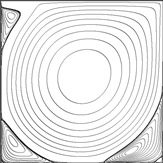
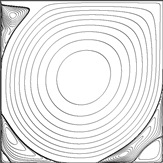
2-D Lid-Driven Cavity Flow Benchmark Solutions
These previously unpublished results are the most accurate steady solutions available for this problem in the range of Re = 1000 - 30000. Velocities and vorticities are provided in table form for selected locations in the flow field. In keeping with tradition, these locations are borrowed from Ghia, 1982 [3] and Botella & Peyret, 1998 [1], but additional ones near the boundaries are included as proposed by Coupez & Hachem, 2013 [9]. All resolved vortex intensities and coordinates are also mapped.
The results for Re = 1000 are of the same accuracy as the spectral solution of Botella & Peyret (converged to 7 digits for the velocities). For the moderate to high Reynolds numbers the solutions are probably one digit less grid-converged, but accuracy should still be at least 1-2 orders of magnitude higher compared to other such data in the literature.
Any further solution detail (for example data at different locations) can be requested via the contact form where you can specify what you need and what it is for.
The results for Re = 1000 are of the same accuracy as the spectral solution of Botella & Peyret (converged to 7 digits for the velocities). For the moderate to high Reynolds numbers the solutions are probably one digit less grid-converged, but accuracy should still be at least 1-2 orders of magnitude higher compared to other such data in the literature.
Any further solution detail (for example data at different locations) can be requested via the contact form where you can specify what you need and what it is for.
Click on each Reynolds number for solution details in PDF
18/2/2025 EDIT: It was recently brought to my attention (thanks goes to Prof. Jean-Luc Guermond from Texas A&M University) that there is a problem with the second to last column in Table 3 (vorticity profile across the horizontal plane at y = 0.95) in the benchmark pdf's. More precisely, the second entry is mistakenly the value at x = 0.995 instead of x = 0.99 (which is instead pushed down the third row) causing the next few entries to be misaligned. Please find the now corrected columns for the respective Reynolds numbers below.
| Table 3 corrected columns (vorticity at y =0.95). | |||||||||
| Re 1000 | Re 2500 | Re 5000 | Re 7500 | Re 10000 | Re 12500 | Re 20000 | Re 25000 | Re 30000 | |
| x | y = 0.95 | y = 0.95 | y = 0.95 | y = 0.95 | y = 0.95 | y = 0.95 | y = 0.95 | y = 0.95 | y = 0.95 |
| 1.0000 | 83.82035 | 124.4745 | 164.5439 | 190.0801 | 208.6591 | 223.3649 | 256.1678 | 273.3864 | 288.7116 |
| 0.9900 | 28.93863 | 11.60644 | -15.48533 | -30.47677 | -37.75954 | -41.17829 | -43.74377 | -43.69902 | -43.27584 |
| 0.9800 | -12.58720 | -23.63701 | -23.09050 | -22.38487 | -21.64013 | -20.75964 | -17.91398 | -16.14544 | -14.55303 |
| 0.9700 | -18.69105 | -16.82244 | -15.68747 | -14.31540 | -12.87952 | -11.55025 | -8.40550 | -6.87469 | -5.65336 |
| 0.9688 | -18.32549 | -16.25095 | -15.09871 | -13.64843 | -12.17661 | -10.84017 | -7.74710 | -6.26765 | -5.09666 |
| 0.9609 | -15.20862 | -13.55147 | -12.00901 | -10.23672 | -8.69272 | -7.41696 | -4.75306 | -3.57529 | -2.67522 |
| 0.9531 | -12.89386 | -11.82738 | -9.90230 | -8.04562 | -6.57244 | -5.42023 | -3.14088 | -2.17635 | -1.46208 |
| 0.9453 | -11.48036 | -10.56168 | -8.40222 | -6.56918 | -5.19755 | -4.15825 | -2.17012 | -1.36717 | -0.80476 |
| 0.9063 | -8.64711 | -7.27447 | -4.89364 | -3.31374 | -2.26655 | -1.56083 | -0.60060 | -0.47653 | -0.54036 |
| 0.8594 | -7.40476 | -5.65664 | -3.19578 | -1.81584 | -1.11327 | -0.81025 | -0.88994 | -1.15565 | -1.39968 |
| 0.8047 | -6.66338 | -4.48919 | -2.01511 | -1.06392 | -0.84706 | -0.92431 | -1.43970 | -1.68308 | -1.82947 |
| 0.6800 | -5.61582 | -2.53771 | -0.87921 | -0.92833 | -1.22799 | -1.48940 | -1.88387 | -1.95128 | -1.95677 |
| 0.5000 | -4.16691 | -0.70297 | -0.52943 | -1.01443 | -1.39683 | -1.65891 | -1.96576 | -1.98142 | -1.95692 |
| 0.3500 | -2.77107 | 0.53550 | 0.48950 | 0.09164 | -0.31583 | -0.68390 | -1.46658 | -1.75677 | -1.92107 |
| 0.2344 | -1.79633 | 2.02107 | 3.36999 | 4.44518 | 5.48332 | 6.50755 | 9.33041 | 10.74982 | 11.63114 |
| 0.2266 | -1.73873 | 2.13815 | 3.62983 | 4.84786 | 6.00703 | 7.10322 | 9.63018 | 10.38588 | 10.40221 |
| 0.1563 | -1.20497 | 2.93612 | 4.80194 | 5.35532 | 5.12516 | 4.55147 | 2.86309 | 2.28026 | 2.12431 |
| 0.0938 | -0.33969 | 2.82240 | 3.96155 | 3.86723 | 3.41940 | 2.94406 | 2.35047 | 2.43886 | 2.58025 |
| 0.0781 | 0.02007 | 2.70749 | 3.69877 | 3.61692 | 3.24928 | 2.87925 | 2.41788 | 2.46935 | 2.57846 |
| 0.0703 | 0.22391 | 2.64670 | 3.57614 | 3.52100 | 3.20714 | 2.88845 | 2.45689 | 2.47963 | 2.57037 |
| 0.0625 | 0.44502 | 2.58307 | 3.46299 | 3.44896 | 3.19528 | 2.92553 | 2.50803 | 2.49477 | 2.56095 |
| 0.0400 | 1.27700 | 2.33570 | 3.19687 | 3.39112 | 3.35613 | 3.24470 | 2.87939 | 2.72977 | 2.65700 |
| 0.0300 | 1.97216 | 2.15464 | 3.02777 | 3.39402 | 3.50997 | 3.51892 | 3.31107 | 3.14237 | 3.00126 |
| 0.0200 | 3.32707 | 2.02655 | 2.44848 | 3.04789 | 3.45164 | 3.69941 | 3.95028 | 3.93747 | 3.86737 |
| 0.0100 | 5.88274 | 2.35162 | 0.53450 | 0.16030 | 0.32588 | 0.72065 | 2.17407 | 3.01380 | 3.67829 |
| 0.0000 | 9.42476 | 3.15380 | -3.61013 | -8.60647 | -12.67382 | -16.13478 | -24.32426 | -28.75590 | -32.73478 |
REFERENCES
[1] O. Botella & R. Peyret, Benchmark spectral results on the lid-driven cavity flow, Computers and Fluids, 27 (1998), pp. 421-433.
[2] A. Shapeev & P. Lin, An asymptotic fitting finite element method with exponential mesh refinement for accurate computation of corner eddies in viscous flows, SIAM Journal of Scientific Computing, 31 (2009), pp. 1874–1900.
[3] U. Ghia, K.N. Ghia & C.T.Shin, High-Re solutions for incompressible flow using the Navier-Stokes equations and a multigrid method, Journal of Computational Physics, 48 (1982), pp. 387-411.
[4] E. Erturk & C. Gokcol, Fourth-order compact formulation of Navier-Stokes equations and driven cavity flow at high Reynolds numbers, International journal for Numerical Methods in Fluids, 50 (2006), pp. 421-436.
[5] R.K. Shukla, M. Tatineni, X. Zhong, Very high-order compact finite difference schemes on non-uniform grids for incompressible Navier-Stokes equations, Journal of Computational Physics, 224 (2007), pp. 1064-1094.
[6] P.N. Shankar & M.D. Deshpande, Fluid mechanics in the driven cavity, Annual Review of Fluid Mechanics, 32 (2000), pp.93-136.
[7] N. Cardoso & P. Bicudo, Time dependent simulation of the driven lid cavity at high Reynolds number, arXiv:0809.3098v2.
[8] E. Hachem, B. Rivaux, T. Kloczko, H. Digonnet, T. Coupez, Stabilized finite element method for incompressible flows with high Reynolds number, Journal of Computational Physics, 229 (2010), pp. 8643-8665.
[9] T. Coupez & E. Hachem, Solution of high-Reynolds incompressible flow with stabilized finite element and adaptive anisotropic meshing, Comput. Methods Appl. Mech. Engrg. , 267 (2013), pp. 65-85.
[10] K. Yapici, Y. Uludag, Finite volume simulation of 2-D steady square lid driven cavity flow at high Reynolds numbers, Brazilian Journal of Chemical Engineering, Vol. 30, No. 4 (2013), pp. 923-937.
[2] A. Shapeev & P. Lin, An asymptotic fitting finite element method with exponential mesh refinement for accurate computation of corner eddies in viscous flows, SIAM Journal of Scientific Computing, 31 (2009), pp. 1874–1900.
[3] U. Ghia, K.N. Ghia & C.T.Shin, High-Re solutions for incompressible flow using the Navier-Stokes equations and a multigrid method, Journal of Computational Physics, 48 (1982), pp. 387-411.
[4] E. Erturk & C. Gokcol, Fourth-order compact formulation of Navier-Stokes equations and driven cavity flow at high Reynolds numbers, International journal for Numerical Methods in Fluids, 50 (2006), pp. 421-436.
[5] R.K. Shukla, M. Tatineni, X. Zhong, Very high-order compact finite difference schemes on non-uniform grids for incompressible Navier-Stokes equations, Journal of Computational Physics, 224 (2007), pp. 1064-1094.
[6] P.N. Shankar & M.D. Deshpande, Fluid mechanics in the driven cavity, Annual Review of Fluid Mechanics, 32 (2000), pp.93-136.
[7] N. Cardoso & P. Bicudo, Time dependent simulation of the driven lid cavity at high Reynolds number, arXiv:0809.3098v2.
[8] E. Hachem, B. Rivaux, T. Kloczko, H. Digonnet, T. Coupez, Stabilized finite element method for incompressible flows with high Reynolds number, Journal of Computational Physics, 229 (2010), pp. 8643-8665.
[9] T. Coupez & E. Hachem, Solution of high-Reynolds incompressible flow with stabilized finite element and adaptive anisotropic meshing, Comput. Methods Appl. Mech. Engrg. , 267 (2013), pp. 65-85.
[10] K. Yapici, Y. Uludag, Finite volume simulation of 2-D steady square lid driven cavity flow at high Reynolds numbers, Brazilian Journal of Chemical Engineering, Vol. 30, No. 4 (2013), pp. 923-937.