My last two posts were really about just a couple of the many experiments I did as part of a project I had been working on. The aim was to design a method for efficient option calibrations of the GARCH diffusion stochastic volatility model. This (and other non-affine) models are usually thought of as impractical for implied (risk-neutral) calibrations because they lack fast semi-analytic (characteristic function-based) vanilla option pricing formulas. But using an efficient PDE-based solver may be an alternative worth looking at. It may prove fast enough to be used for practical calibrations, or at the very least provide insight on the overall performance of (non-affine) models that have seen increased interest in recent years. Besides, analytical tractability definitely shouldn't the main criterion for choosing a model.
For those interested there's now a detailed report of this joint collaboration with Alan Lewis on the arXiv: A First Option Calibration of the GARCH Diffusion Model by a PDE Method. Alan's blog can be found here.
For those interested there's now a detailed report of this joint collaboration with Alan Lewis on the arXiv: A First Option Calibration of the GARCH Diffusion Model by a PDE Method. Alan's blog can be found here.
EDIT: For the results reported in the paper, Excel's solver was used for the optimization. I've now quickly plugged the PDE engine into M. Lourakis' Levenberg-Marquardt implementation (levmar) and built a basic demo so that perhaps people can try to calibrate the model to their data. It doesn't offer many options, just a fast / accurate switch. The fast option is typically plenty accurate as well. So, if there's some dataset you may have used for calibrating say the Heston model, it would be interesting to see how will the corresponding GARCH diffusion fit compare. Irrespective of the fit, GARCH diffusion is arguably a preferable model, not least because it typically implies more plausible dynamics than Heston. Does this also translate to more stable parameters on recalibrations? Are the fitted (Q-measure) parameters closer to those obtained from the real (P-measure) world? If the answers to the above questions are mostly positive, then coupling the model with local volatility and/or jumps could give a better practical solution than what the industry uses today. (Of course one could just as easily do that with the optimal-p model instead of GARCH diffusion, as demonstrated in my previous post.) Something for the near future.
If you do download the calibrator and use it on your data, please do share your findings (or any problems you may encounter), either by leaving a comment below, or by sending me an email. As a bonus, I've also included the option to calibrate another (never previously calibrated) non-affine model, the general power-law model with p = 0.8 (sitting between Heston and GARCH diffusion, see [1]).
If you do download the calibrator and use it on your data, please do share your findings (or any problems you may encounter), either by leaving a comment below, or by sending me an email. As a bonus, I've also included the option to calibrate another (never previously calibrated) non-affine model, the general power-law model with p = 0.8 (sitting between Heston and GARCH diffusion, see [1]).
Note that (unless you have Visual Studio 2013 installed) you will also need to download the VC++ Redistributable for VS2013. The 64-bit version (which is a little faster) also requires the installation of Intel's MKL library.
EDIT April 2020: After downloading and running this on my new Windows 10 laptop I saw that the console was not displaying the inputs as intended (it was empty). To get around this please right click on the top of the console window, then click on Properties and there check "Use legacy console". Then close the console and re-launch.
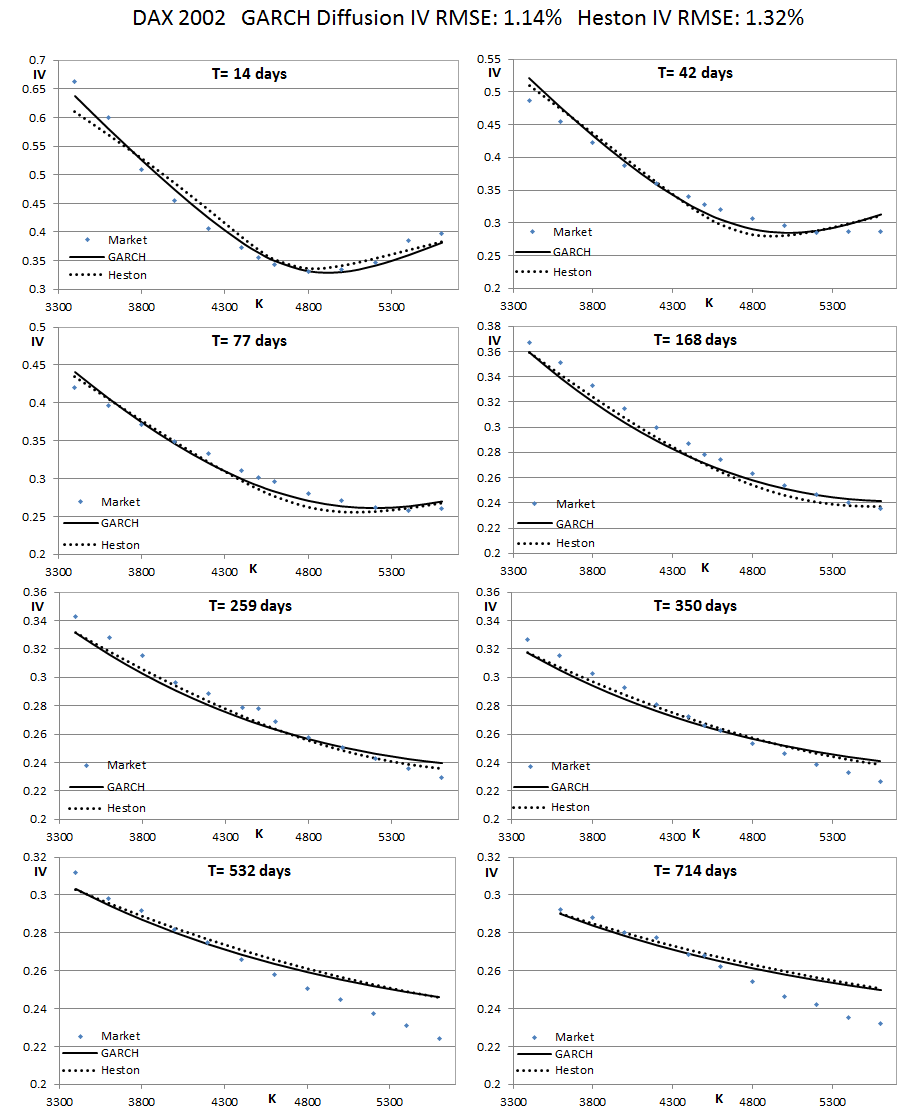
I am also including in the download a sample dataset I found in [2] (DAX index IV surface from 2002), so that you can readily test the calibrator. I used it to calibrate both Heston (also calibrated in [2], together with many other affine models) and GARCH diffusion. In contrast to the two datasets we used in the paper, in this case GARCH diffusion (RMSE = 1.14%) "beats" Heston (RMSE = 1.32%). This calibration takes about 5 secs. This is faster than the times we report on the paper and the reason is that the data we considered there include some very far out-of-the-money options that slow things down as they require higher resolution. The Levenberg-Marquardt algo is also typically faster than Excel's solver for this problem. It is also "customizable", in the sense that one can adjust the grid resolution during the calibration based on the changing (converging) parameter vector. Still, this version is missing a further optimization that I haven't implemented yet, that I expect to reduce the time further by a factor of 2-3.
EDIT April 2020: After downloading and running this on my new Windows 10 laptop I saw that the console was not displaying the inputs as intended (it was empty). To get around this please right click on the top of the console window, then click on Properties and there check "Use legacy console". Then close the console and re-launch.
I am also including in the download a sample dataset I found in [2] (DAX index IV surface from 2002), so that you can readily test the calibrator. I used it to calibrate both Heston (also calibrated in [2], together with many other affine models) and GARCH diffusion. In contrast to the two datasets we used in the paper, in this case GARCH diffusion (RMSE = 1.14%) "beats" Heston (RMSE = 1.32%). This calibration takes about 5 secs. This is faster than the times we report on the paper and the reason is that the data we considered there include some very far out-of-the-money options that slow things down as they require higher resolution. The Levenberg-Marquardt algo is also typically faster than Excel's solver for this problem. It is also "customizable", in the sense that one can adjust the grid resolution during the calibration based on the changing (converging) parameter vector. Still, this version is missing a further optimization that I haven't implemented yet, that I expect to reduce the time further by a factor of 2-3.
The fitted parameters are:
GARCH: v0 = 0.1724, vBar = 0.0933, kappa = 7.644, xi = 7.096, rho = -0.5224.
Heston: v0 = 0.1964, vBar = 0.0744, kappa = 15.78, xi = 3.354, rho = -0.5118.
Note that both models capture the short-term smile/skew pretty well (aided by the large fitted xi's, aka vol-of-vols), but then result in a skew that decays (flattens) too fast for the longer expirations.
References
[1] Y. Papadopoulos, A. Lewis, “A First Option Calibration of the GARCH Diffusion Model by a PDE Method.,” arXiv:1801.06141v1 [q-fin.CP], 2018.
[2] Kangro, R., Parna, K., and Sepp, A., (2004), “Pricing European Style Options under Jump Diffusion Processes with Stochastic Volatility: Applications of Fourier Transform,” Acta et Commentationes Universitatis Tartuensis de Mathematica 8, 123-133.
[2] Kangro, R., Parna, K., and Sepp, A., (2004), “Pricing European Style Options under Jump Diffusion Processes with Stochastic Volatility: Applications of Fourier Transform,” Acta et Commentationes Universitatis Tartuensis de Mathematica 8, 123-133.
 RSS Feed
RSS Feed